 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Гипербола
Определение. Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Обозначим фокусы гиперболы через F 1 и F 2 (рис. 41). Пусть М – произвольная точка гиперболы. Расстояние | F 1 F 2| между фокусами обозначим через 2 с, а модуль разности расстояний от точки М до фокусов – через 2 а. Так как по определению || F 1 M | – | F 2 M || < | F 1 F 2|, то 2 а < 2 с или а < с. Числа | F 1 M | и | F 2 M | называются фокальными радиусами точки М и обозначаются через r 1 и r 2. Из определения следует, что точка М (х; у) лежит на данной гиперболе тогда и только тогда, когда | r 1 – r 2|= 2 a. Отсюда r 1 – r 2 = ±2 a. (9) По аналогии с эллипсом, чтобы получить искомое уравнение гиперболы, нужно в равенстве (9) заменить переменные r 1 и r 2 их выражениями через координаты х и у. Так как фокусы F 1 и F 2 расположены на оси Ox симметрично относительно начала координат, то они имеют соответственно координаты (– с; 0) и (с; 0). По формуле расстояния между двумя точками находим
Подставив эти выражения в равенство (9), получим
Это и есть искомое уравнение гиперболы. Упростим его аналогично тому, как это было сделано для уравнения (3) в случае эллипса. Перенесем второй радикал в правую часть уравнения (11), а затем возведем обе части полученного равенства в квадрат. Имеем (x + c)2 + y 2 = 4 a 2 ± или cx – a 2 = ± a Снова возведем обе части равенства в квадрат: a 4 – 2 a 2 cx + c 2 x 2 = a 2 x 2 – 2 a 2 cx + a 2 c 2 + a 2 y 2. Отсюда (c 2 – a 2) x 2 – a 2 y 2 = a 2(c 2 – a 2). (13) Рассмотрим теперь новую величину
геометрический смысл которой будет раскрыт далее. Так как с > а, то разность c 2 – a 2 > 0 и b – положительное число. Из равенства (14) имеем b 2 = c 2 – a 2. Поэтому уравнение (13) примет вид b 2 x 2 – a 2 y 2 = a 2 b 2 или
Это и есть каноническое уравнение гиперболы. Как и для эллипса, можно доказать равносильность уравнений (15) и (11). Исследуем форму гиперболы по ее каноническому уравнению. Так как уравнение (15) содержит члены только с четными степенями текущих координат х и у, то по аналогии с эллипсом достаточно рассмотреть лишь часть гиперболы, лежащую в I координатном угле. Разрешим уравнение (15) относительно у, считая у
Из равенства (16) вытекают следующие утверждения: 1) если 0 2) если х = а, то у = 0, т. е. точка А (а; 0) принадлежит гиперболе; 3) если х > а, то у > 0. При возрастании х значение у также возрастает и у → +∞ при х → +∞. Переменная точка М (х; у) на гиперболе перемещается с ростом х «вправо» и «вверх», причем ее начальное положение – точка А (а; 0) (рис. 42). Здесь необходимо уточнить, как именно точка М «уходит в бесконечность». Для этого, кроме уравнения (16), рассмотрим уравнение
которое определяет прямую с угловым коэффициентом k = b / a, проходящую через начало координат. Часть этой прямой, расположенная в I координатном угле, изображена на рис. 42. Для ее построения можно использовать прямоугольный треугольник ОАВ,где | OA | = a и | AB | = b. Покажем, что точка М, перемещаясь по гиперболе в бесконечность, неограниченно приближается к прямой (17), которая является асимптотой гиперболы. Возьмем произвольное значение х (x Прежде всего заметим, что если x > a, то
Это означает, что при одной и той же абсциссе точка гиперболы лежит под соответствующей точкой асимптоты. Таким образом, MN = Y – y =
Из полученного выражения следует, что при х → +∞ дробь стремится к нулю, так как знаменатель растет, а числитель – постоянная величина ab. Следовательно, | MN| = Y – y стремится к нулю при х → +∞. Обозначим через Р основание перпендикуляра, опущенного из точки М на прямую (17), МР – расстояние от точки М до этой прямой. Очевидно, | MP | < | MN |, а так как | MN | → 0, то и подавно | MP | → 0 при х → +∞, т.е. точка М неограниченно приближается к прямой (17), а это нам и требовалось доказать. Аналогичное рассуждение можно провести для любого координатного угла. Итак, ветвь рассматриваемой гиперболы, лежащая в I координатном угле, проходит через точку А (а; 0) и направлена «направо» и «вверх», асимптотически приближаясь к прямой
Оси симметрии называются осями гиперболы, а центр симметрии (точка пересечения осей) – центром гиперболы. Одна из осей пересекается с гиперболой в двух точках, которые называются ее вершинами (на рис. 44 они обозначены буквами А ′ и А). Эта ось называется действительной осью гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью гиперболы. Прямоугольник ВВ ′ C ′ C со сторонами 2 а и 2 b (рис. 44) называется основным прямоугольником гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы. Уравнение
переставляя буквы х и у, а и b, можно привести к виду (15). Отсюда ясно, что уравнение (18) определяет гиперболу, расположенную так, как показано на рис. 44 штриховыми линиями; вершины ее лежат на оси Oy. Эта гипербола называется сопряженной по отношению к гиперболе (15). Обе гиперболы имеют одни и те же асимптоты. Гипербола с равными полуосями (а = b) называется равносторонней, и ее каноническое уравнение имеет вид x 2 – y 2 = a 2. (19) Так как основной прямоугольник равносторонней гиперболы является квадратом, то асимптоты равносторонней гиперболы перпендикулярны друг другу. Определение. Эксцентриситетом гиперболы является отношение с / а, где с – половина расстояния между фокусами, а – действительная полуось гиперболы. Эксцентриситет гиперболы (как и эллипса) обозначим буквой ε. Так как с > а, то ε > 1, т. е. эксцентриситет гиперболы больше единицы. Учитывая, что c 2 = a 2 + b 2, найдем
откуда
Из последнего равенства легко получить геометрическое истолкование эксцентриситета гиперболы. Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше отношение b / а, что означает, что основной прямоугольник более вытянут в направлении действительной оси. Таким образом, эксцентриситет характеризует форму ее основного прямоугольника, а значит, и форму самой гиперболы. Для равносторонней гиперболы (а = b) получаем Пример. Дано уравнение гиперболы 3 x 2 – 4 y 2 = 12. Найти ее действительную и мнимую полуоси, координаты фокусов, эксцентриситет; составить уравнение ее асимптот. Решение. Приведем уравнение гиперболы к каноническому виду:
откуда находим, что действительная полуось а = 2, а мнимая полуось b = В следующем пункте рассмотрим важное свойство эллипса и гиперболы.
Дата добавления: 2015-01-18 | Просмотры: 1643 | Нарушение авторских прав |
 Для вывода уравнения гиперболы введем на плоскости прямоугольную систему координат так, чтобы фокусы гиперболы лежали на оси абсцисс, а начало координат делило бы расстояние между фокусами пополам. Выведем уравнение гиперболы в выбранной системе координат.
Для вывода уравнения гиперболы введем на плоскости прямоугольную систему координат так, чтобы фокусы гиперболы лежали на оси абсцисс, а начало координат делило бы расстояние между фокусами пополам. Выведем уравнение гиперболы в выбранной системе координат.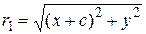 ,
, 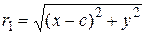 . (10)
. (10) –
– 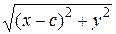 = ±2 a. (11)
= ±2 a. (11)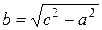 , (14)
, (14)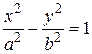 . (15)
. (15)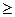 0:
0: . (16)
. (16) x < a, то у принимает мнимые значения, т. е. точек гиперболы с абсциссами 0
x < a, то у принимает мнимые значения, т. е. точек гиперболы с абсциссами 0  x < a не существует;
x < a не существует;
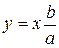 , (17)
, (17) . Точка М лежит на ги
. Точка М лежит на ги  перболе, точка N – на прямой (17). Так как обе точки имеют одну и ту же абсциссу х, то прямая, проходящая через точки М и N, перпендикулярна оси Оx (рис. 43). Найдем длину отрезка МN.
перболе, точка N – на прямой (17). Так как обе точки имеют одну и ту же абсциссу х, то прямая, проходящая через точки М и N, перпендикулярна оси Оx (рис. 43). Найдем длину отрезка МN. >
>  .
.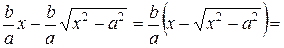
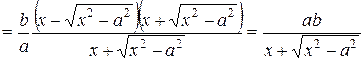 .
. (см. рис. 42).
(см. рис. 42). Теперь можно легко установить вид всей гиперболы в силу ее симметрии относительно координатных осей (рис. 44). Гипербола состоит из двух ветвей (правой и левой) и имеет две асимптоты:
Теперь можно легко установить вид всей гиперболы в силу ее симметрии относительно координатных осей (рис. 44). Гипербола состоит из двух ветвей (правой и левой) и имеет две асимптоты:  и
и 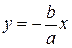 , первая из которых уже рассмотрена, а вторая представляет собой ее симметрическое отражение относительно оси Оx (или оси Oy).
, первая из которых уже рассмотрена, а вторая представляет собой ее симметрическое отражение относительно оси Оx (или оси Oy). , (15)
, (15)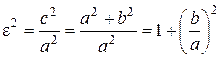
 .
.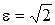 .
.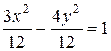 или
или 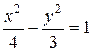
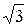 . Так как асимптоты гиперболы имеют уравнения
. Так как асимптоты гиперболы имеют уравнения  , фокусы – координаты (– с; 0) и (с; 0), эксцентриситет ε = c / a, а
, фокусы – координаты (– с; 0) и (с; 0), эксцентриситет ε = c / a, а  , то для данной гиперболы получаем: координаты фокусов
, то для данной гиперболы получаем: координаты фокусов  и
и 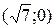 ; эксцентриситет
; эксцентриситет  и уравнения асимптот
и уравнения асимптот 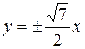 .
.