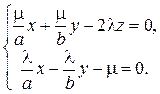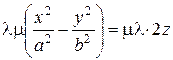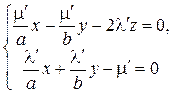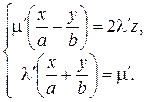|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Поверхностей второго порядка
В этом параграфе будем предполагать систему координат прямоугольной.
1. распадающиеся поверхности Если многочлен второй степени F (х, у, z) есть произведение двух многочленов первой степени F (x, y, z) = (A 1 x + B 1 y + C 1 z + D 1)(A 2 x + B 2 y + C 2 z + D 2), то поверхность F (x, y, z) = 0 распадается на пару плоскостей π1: A 1 x + B 1 y + C 1 z + D 1 = 0 и π2: A 2 x + B 2 y + C 2 z + D 2 = 0. Если эти плоскости пересекаются, то сделаем прямую их пересечения осью аппликат, а биссекторные плоскости двугранных углов, образуемых этими плоскостями, примем за координатные плоскости yOz и xOz прямоугольной системы координат, беря в качестве плоскости xOy любую плоскость, перпендикулярную к линии пересечения данных плоскостей. В полученной системе координат плоскости π1 и π2 получают уравнения Ax + By = 0 и Ax – By = 0, а поверхность F (х, у, z) = 0, распавшаяся на эти плоскости, будет поверхностью (Ax + By)(Ax – By) = 0, или A 2 x 2 – B 2 y 2 = 0. (32) Всякая поверхность второго порядка, распадающаяся на пару пересекающихся плоскостей, в некоторой системе координат имеет уравнение (32). Если поверхность распадается на пару параллельных плоскостей π1 и π2, то примем за плоскость xОy прямоугольной системы координат O и векторы e 1 и e 2 возьмем в плоскости π, а вектор e 3 направим перпендикулярно к плоскости π, тогда плоскости π1 и π2 будут соответственно иметь уравнения z = a и z = – a, а уравнение пары плоскостей π1, π2 будет z 2 – a 2 = 0. Уравнение (Ax + By + Cz + D)2 = 0 определяет пару совпадающих между собой плоскостей Ax + By + Cz + D = 0. Приняв эту плоскость за плоскость z = 0 новой координатной системы, мы видим, что всякая поверхность второго порядка, являющаяся парой совпадающих между собой плоскостей, в некоторой системе координат может быть задана уравнением z 2 = 0. Поверхность, распадающаяся на пару мнимых (сопряженных) плоскостей, может быть задана уравнением A 2 x 2 + B 2 y 2 = 0, если эти плоскости пересекаются, и уравнением z 2 + a 2 = 0, если они параллельны.
2. цилиндрические поверхности Цилиндрическая поверхность второго порядка задается в некоторой, надлежаще выбранной для данной поверхности, канонической системе координат уравнением F (х, у) = 0, (33) где F (х, у) – многочлен второй степени от переменных х и у. Кривая, определенная уравнением (33) в плоскости xOy, является направляющей кривой (основанием) цилиндрической поверхности. Эта кривая может быть эллипсом, действительным или мнимым, гиперболой или параболой, в зависимости от чего мы и различаем эллиптические, мнимые эллиптические, гиперболические и параболические цилиндры, канонические уравнения которых совпадают с каноническими уравнениями их направляющих кривых (33). Если направляющая (33) есть пара прямых, то цилиндрическая поверхность вырождается в пару плоскостей (пересекающихся, параллельных или совпадающих, действительных или мнимых – в зависимости от соответствующего свойства лежащей в основании пары прямых).
3. поверхности вращения Поверхность S называется поверхностью вращения с осью d, если она составлена из окружностей, которые имеют центры на прямой d и лежат в плоскостях, перпендикулярных этой прямой.
Выберем начало декартовой прямоугольной системы координат O на оси вращения d, вектор e 3 направлен вдоль d, а вектор e 1 поместим в плоскости P. Таким образом, точка О и векторы e 1 и e 3 образуют на плоскости P декартову систему координат. Очевидно, вектор e 2 выбираем таким образом, чтобы тройка векторов e 1, e 2, e 3 была правой. Допустим, что линия L, вращением которой получена поверхность, имеет в этой системе координат уравнение φ(x, z) = 0. Рассмотрим точку М (х; у; z), лежащую на поверхности вращения. Через нее проходит окружность, которая имеет центр на оси d и лежит в плоскости, перпендикулярной этой оси. Радиус окружности равен расстоянию от М до оси, т. е. Точка M 1(x 1, y 1, z 1) лежит в плоскости Р и потому y 1 = 0. Учитывая, что M 1 и М лежат на одной окружности, перпендикулярной оси e 3, то z 1 = z и | x 1| = Подставляя в это уравнение x 1 и z 1, мы получаем следующее условие на координаты точки М, необходимое и достаточное для того, чтобы М лежала на поверхности вращения S:
Это равенство должно быть выполнено хотя бы при одном из двух знаков перед корнем. Это условие, которое может быть записано в эквивалентном виде:
и является уравнением поверхности вращения линии L вокруг оси d.
4. эллипсоид Рассмотрим поверхности, которые получаются при вращении эллипса вокруг его осей симметрии. Направим вектор e 3 сначала вдоль его малой оси эллипса (рис. 55), а затем вдоль большой оси (рис. 56). Получим уравнение эллипса в следующих видах:
И, следовательно, уравнения поверхностей будут:
Поверхности, описываемые уравнениями (35), называются сжатым и вытянутым эллипсоидами вращения. Каждую точку М (х; у; z) на эллипсоиде вращения сдвинем к плоскости xOz так, чтобы расстояние от точки до этой плоскости уменьшилось в постоянном для всех точек отношении λ < 1. После сдвига точка М совпадает с точкой M ′, координаты которой определяются равенствами x ′ = x, y ′ = λ y, z ′ = z. Таким образом, все точки эллипсоида вращения (35) переходят в точки поверхности с уравнением
где b = λ a. Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение (36), назовем эллипсоидом. Положительные числа а, b, с называются полуосями эллипсоида (36). Эллипсоид лежит внутри прямоугольного параллелепипеда
Другими словами, эллипсоиды суть ограниченные поверхности. Все плоские сечение эллипсоида являются ограниченными кривыми второго порядка – эллипсами. Поверхность, задаваемая в какой-нибудь прямоугольной системе координат уравнением
называется мнимым эллипсоидом. Мнимый эллипсоид не имеет ни одной вещественной точки. Очевидно, что сфера является частным случаем эллипсоида, когда все полуоси равны между собой:
Это уравнение сферы с центром в начале координат и радиусом а.
5. конус второго порядка Рассмотрим на плоскости Р пару пересекающихся прямых, задаваемую в системе координат О, e 1, e 3 уравнением a 2 x 2 – c 2 z 2 = 0. Поверхность, получаемая вращением этой линии вокруг оси аппликат, имеет уравнение a 2 (x 2 + y 2) – c 2 z 2 = 0 и носит название прямого кругового конуса. Сжатие к плоскости xOz переводит прямой круговой конус в поверхность с уравнением: a 2 x 2 + b 2 y 2 – c 2 z 2 = 0. (37) Поверхность, которая в некоторой прямоугольной декартовой системе координат имеет уравнение (37), называется конусом или конусом второго порядка. Конус состоит из прямых линий, проходящих через начало координат (рис. 57).
a 2 x 2 + b 2 y 2 – c 2α2 = 0, a 2 x 2 + b 2 y 2 = c 2α2, делим уравнение на c 2α2:
Обозначив
Плоскости, параллельные плоскостям xOz и yOz, пересекают конус по гиперболам. Действительно, пусть x = β, тогда имеем a 2 β 2 + b 2 y 2 – c 2 z 2 = 0, b 2 y 2 – c 2 z 2 = – a 2 β 2. Умножим это уравнение на (–1), получим c 2 z 2 – b 2 y 2 = a 2 β 2. Разделим это уравнение на a 2 β 2:
Обозначив
т. е. в сечении конуса плоскостью x = β лежит гипербола. Аналогичный результат можно получить, рассматривая сечения конуса плоскостями, параллельными плоскости xOz. Не только эллипс и гипербола, но и парабола являются плоскими сечениями конуса. Для простоты рассмотрим круговой конус x 2 + y 2 – z 2 = 0. (38) Докажем, что параболой является, например, сечение конуса (38) плоскостью π, заданной уравнением x – z + 1 = 0. Выразим z = х + 1 из уравнения плоскости и подставим в уравнение конуса (38): x 2 + y 2 – (x + 1)2 = 0, x 2 + y 2 – x 2 – 2 x – 1 = 0, y 2 = 2 x + 1, y 2 = 2(x + 0,5). Обозначив x + 0,5 = x ′, получаем уравнение параболы: y 2 = 2 x ′. Итак, и эллипс, и гипербола, и парабола являются сечениями конуса. Поэтому эти кривые и называются коническими сечениями. Наряду с действительными конусами второго порядка существуют еще мнимые конусы, которые в канонической для них системе координат имеют уравнение
Единственная действительная точка мнимого конуса есть точка начала координат О (0; 0; 0). Заметим, что цилиндрические и канонические поверхности второго порядка объединяются под общим наименованием вырождающихся поверхностей второго порядка; им, в качестве невырождающихся поверхностей, противополагаются эллипсоиды, гиперболоиды и параболоиды.
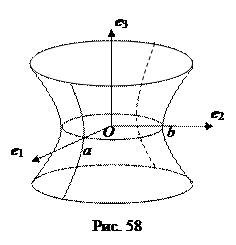
6. однополостный гиперболоид Однополостный гиперболоид вращения – это поверхность вращения гиперболы
вокруг мнимой полуоси (той оси, которая ее не пересекает). Для того чтобы от уравнения кривой перейти к уравнению поверхности, заменим х на
Это уравнение однополостного гиперболоида вращения.
Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение (39), называется однополостным гиперболоидом (рис. 58). Положительные числа а, b и с называются полуосями гиперболоида. Если вместе с гиперболой мы будем вращать и ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. При сжатии гиперболоида вращения в общий однополостный гиперболоид прямой круговой конус сжимается в некоторый конус, который называется асимптотическим конусом однополостного гиперболоида. Из уравнения (39) видно, что начало канонической для данного гиперболоида системы координат является его центром симметрии, координатные плоскости прямоугольной канонической системы – его плоскостями симметрии, а оси координат этой системы – осями симметрии. Если а = b = с, то гиперболоид называется правильным. Плоскость z = h пересекает однополостный гиперболоид (39) по кривой
Положим
Все эти эллипсы подобны между собой, отношения их полуосей
одно и то же, их эксцентриситеты равны эксцентриситету эллипса
являющегося пересечением однополостного гиперболоида (39) с плоскостью z = 0; этот эллипс называется горловым эллипсом данного однополостного гиперболоида. Сечения однополостного гиперболоида (39) плоскостями y = β есть кривые
Полагая
Аналогично можно доказать, что сечения однополостного гиперболоида плоскостями x = α также будут гиперболами. Сечение однополостного гиперболоида (39) каждой из плоскостей y = ± b есть пара прямых
Точно так же сечение однополостного гиперболоида (39) каждой из плоскостей x = ± a есть пара прямых
Интересное свойство однополостного гиперболоида – наличие у него прямолинейных образующих (рис. 59). Прямолинейные образующие – прямые линии, всеми своими точками лежащие на поверхности. Через каждую точку однополостного гиперболоида проходят две прямолинейные образующие. Докажем это и получим уравнение прямолинейных образующих. В уравнении однополостного гиперболоида
перенесем второе слагаемое в правую часть
и разделим обе части равенства на множители:
Рассмотрим теперь прямую линию, заданную как пересечение двух плоскостей:
где μ и λ – некоторые числа. Легко преобразовать эти уравнения к привычному виду плоскостей:
Координаты каждой точки прямой удовлетворяют обоим уравнениям, а, следовательно, и их произведению – уравнению (39). Поэтому все точки прямых линий с уравнениями вида (41) при всевозможных λ и μ лежат на однополостном гиперболоиде. Такое же рассуждение можно провести и для семейства прямых
Подставляя координаты точки, лежащей на однополостном гиперболоиде, в одно из уравнений (41) и в одно из уравнений (42), мы найдем значения параметров λ, μ и λ′, μ′, которые соответствуют прямолинейным образующим, проходящим через эту точку. Естественно, что каждая пара параметров определена с точностью до общего множителя.
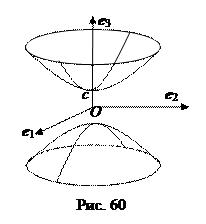
7. двуполостный гиперболоид Двуполостный гиперболоид вращения – это поверхность вращения гиперболы
вокруг той оси, которая ее пересекает (вокруг действительной оси).
В результате сжатия этой поверхности получается поверхность, задаваемая уравнением
Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение вида (44), называется двуполостным гиперболоидом. Двум ветвям гиперболы здесь соответствуют две несвязанные между собой части («полости») поверхности, в то время как при построении однополостного гиперболоида вращения каждая ветвь гиперболы описывает всю поверхность (рис. 60).
Рассмотрим теперь пересечения двуполостного гиперболоида (44) с плоскостями, параллельными координатным. Плоскость z = h при | h | < c пересекает поверхность (44) по мнимым эллипсам, при | h | > c по вещественным. Если а = b, то эти эллипсы являются окружностями, а гиперболоид – есть гиперболоид вращения. При | h | = c получаем
т. е. пару сопряженных прямых с одной вещественной точкой (0; 0; с) (или (0; 0; – с) соответственно). Плоскости x = α и y = β пересекают гиперболоид (44) по гиперболам
8. эллиптический параболоид При вращении параболы x 2 = 2 pz вокруг ее оси симметрии получим поверхность с уравнением x 2 + y 2 = 2 pz,
Поверхность, которая имеет такое уравнение в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом. Внешний вид эллиптического параболоида ясен из способа его построения. Он весь расположен по одну сторону от плоскости z = 0, в полупространстве z > 0 (рис. 62). Сечения плоскостями z = h, h > 0 имеют уравнение:
или
и являются эллипсами. Сечения эллиптического параболоида (45) плоскостями у = 0 и х = 0 являются параболами x 2 = 2 a 2 z, y = 0; (46) y 2 = 2 b 2 z, x = 0. (47) Эти параболы называют главными параболами эллиптического параболоида, при этом параболу (46) условно назовем неподвижной, а параболу (47) – подвижной. Можно дать следующее очень наглядное построение эллиптического параболоида посредством скольжения одной параболы вдоль другой (система координат предполагается прямоугольной). Возьмем сечение параболоида (45) плоскостью x = α, получим в этой плоскости, содержащей систему координат O 0 e 2 e 3, где O 0 = (α, 0, 0), кривую, уравнение которой будет
или y 2 = 2 b 2(z – γ), x = α, (48) где Перейдем в плоскости x = α от системы координат O e 2 e 3 к системе координат O ′ e 2 e 3, где O ′ = (α, 0, γ) есть точка пересечения плоскости x = α с неподвижной параболой x 2 = 2 a 2 z, y = 0. Перенеся начало координат системы O 0 e 2 e 3 в точку O ′, произвели следующее преобразование координат: y = y ′, z = z ′ + γ. В результате этого преобразования уравнение (48) получает вид: y ′2 = 2 pz ′, x = α. Кривая (48) – это та же «подвижная» парабола, но перенесенная параллельно себе в плоскость x = α. Этот перенос можно осуществить следующим образом. Вершина подвижной параболы скользит по неподвижной параболе из точки О в точку O ′, а сама парабола при этом перемещается, как твердое тело, оставаясь все время в плоскости, параллельной плоскости yOz. Этот результат можно сформулировать в виде следующего утверждения. Эллиптический параболоид есть поверхность, описываемая при движении одной («подвижной») параболы (47) вдоль другой, неподвижной (46), так, что вершина подвижной параболы скользит по неподвижной, а плоскость и ось подвижной параболы остаются все время параллельными самим себе, причем предполагается, что обе параболы (подвижная и неподвижная) обращены вогнутостью в одну и ту же сторону (а именно в положительную сторону оси Oz). Заметим, что эллиптический параболоид прямолинейных образующих не имеет. Действительно, прямая, параллельная плоскости xOy, может пересекать лишь сечение параболоида некоторой плоскостью z = h, а это сечение, как уже было отмечено, представляет собой эллипс. И значит, у прямой не более двух общих точек с параболоидом. Если же прямая не параллельна плоскости xOy, то ее полупрямая лежит в полупространстве z < 0, где нет ни одной точки параболоида. Таким образом, нет прямой, которая всеми своими точками лежала бы на эллиптическом параболоиде.
9. гиперболический параболоид По аналогии с уравнением (45) можем записать уравнение
Поверхность, которая имеет в некоторой системе координат уравнение вида (49) назовем гиперболическим параболоидом.
Для больших значений h полуоси гиперболы При h = 0 гипербола вырождается в пару пересекающихся прямых
или
Если h < 0, то ось гиперболы, которая ее пересекает, параллельна вектору e 2. Полуоси растут с увеличением | h |. Отношение полуосей для всех гипербол при одном знаке h одно и то же. Поэтому, если мы нарисуем все сечения гиперболического параболоида на одной и той же плоскости, то получим семейство всех гипербол, имеющих в качестве асимптот пару пересекающихся прямых с уравнениями
Сечения гиперболического параболоида с плоскостями у = 0 и х = 0 являются двумя «главными параболами»: x 2 = 2 a 2 z, y = 0 (50) – неподвижная парабола, и y 2 = –2 b 2 z, x = 0 (51) – подвижная парабола. Эти параболы обращены вогнутостью в противоположные стороны: неподвижная – «вверх» (т.е. в положительном направлении оси Oz), а подвижная – «вниз» (т.е. в отрицательном направлении оси Oz). Сечение в плоскости x = α имеет в системе координат O 0 e 2 e 3, где O 0 = (α, 0, 0), уравнение
или y 2 = –2 b 2(z – z 0), x = α, (52) где После перенесения начала координат в точку O ′ = (α, 0, z 0), уравнение (51) примет вид: y ′2 = –2 b 2 z ′, x = α, где y = y ′, z = z ′ + z 0. Последнее уравнение показывает, что кривая (52) – это та же подвижная парабола (51), только сдвинутая параллельно себе при скольжении ее вершины вдоль неподвижной параболы из точки О в O ′. Отсюда вытекает следующее утверждение. Гиперболический параболоид, заданный (в прямоугольной системе координат) уравнением (49) есть поверхность, описываемая параболой y 2 = –2 b 2 z, х = 0 при ее движении вдоль неподвижной параболы (50) так, что вершина подвижной параболы скользит по неподвижной параболе, а плоскость и ось подвижной параболы остаются все время параллельными себе самим, при этом обе параболы вогнутостью все время обращены в противоположные стороны: неподвижная – вогнутостью «вверх», т. е. в положительном направлении оси Из этого построения видно, что гиперболический параболоид имеет вид седла. Гиперболический параболоид, как и однополостной гиперболоид, имеет два семейства прямолинейных образующих (рис. 64). Через каждую точку гиперболического параболоида проходят две прямые, которые всеми точками лежат на этой плоскости. Найдем уравнения прямолинейных образующих. Перепишем уравнение (49) в виде
Рассмотрим прямую, заданную как пересечение двух плоскостей
или
Очевидно, что любая точка, удовлетворяющая уравнениям (53), удовлетворяет и уравнению (49), которое является произведением уравнений (53)
или
А это значит, что каждая точка прямой (53) принадлежит гиперболическому параболоиду (49). Аналогично рассматривается прямая
или
Прямая (54) также всеми своими точками лежит на гиперболическом параболоиде.
Дата добавления: 2015-01-18 | Просмотры: 1605 | Нарушение авторских прав |
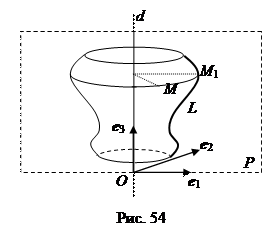 Рассмотрим линию L, которая лежит в плоскости P, проходящей через ось вращения d, и будем вращать ее вокруг этой оси (рис. 54). Каждая точка линии опишет окружность, а вся линия – поверхность вращения.
Рассмотрим линию L, которая лежит в плоскости P, проходящей через ось вращения d, и будем вращать ее вокруг этой оси (рис. 54). Каждая точка линии опишет окружность, а вся линия – поверхность вращения.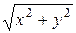 . Точка М лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка M 1, принадлежащая вращаемой линии L.
. Точка М лежит на поверхности вращения тогда и только тогда, когда на указанной окружности имеется точка M 1, принадлежащая вращаемой линии L.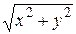 .Координаты точки M 1 удовлетворяют уравнению линии L: φ(x 1, z 1) = 0.
.Координаты точки M 1 удовлетворяют уравнению линии L: φ(x 1, z 1) = 0.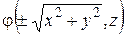 = 0. (34)
= 0. (34)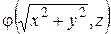
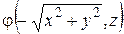 = 0
= 0
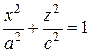 ,
, 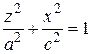 .
.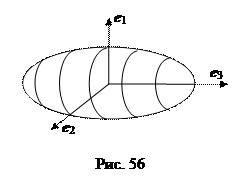 (Здесь через с обозначена малая полуось эллипса.) В силу формулы (34) для того, чтобы перейти к уравнениям соответствующих поверхностей вращения, мы должны заменить х на
(Здесь через с обозначена малая полуось эллипса.) В силу формулы (34) для того, чтобы перейти к уравнениям соответствующих поверхностей вращения, мы должны заменить х на 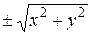 в уравнении кривой. Получаем
в уравнении кривой. Получаем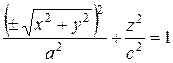 ,
, 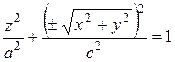 .
. ,
,  . (35)
. (35)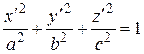 , (36)
, (36)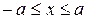 ,
,  ,
, 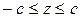 .
.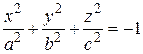
 или x 2 + y 2 + z 2 = a 2.
или x 2 + y 2 + z 2 = a 2. Рассмотрим сечения конуса плоскостями. Плоскость, параллельная плоскости xOy, z = α пересекает конус по эллипсу. Действительно,
Рассмотрим сечения конуса плоскостями. Плоскость, параллельная плоскости xOy, z = α пересекает конус по эллипсу. Действительно,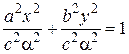 =>
=> 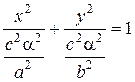 .
.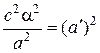 и
и 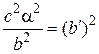 , получаем уравнение эллипса:
, получаем уравнение эллипса: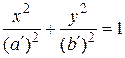 .
.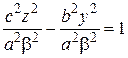 =>
=>  .
.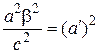 ;
; 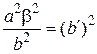 видим, что
видим, что ,
,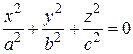 .
.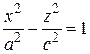
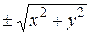 , получим
, получим =>
=> 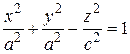 .
. В результате сжатия этой поверхности мы получаем поверхность с уравнением
В результате сжатия этой поверхности мы получаем поверхность с уравнением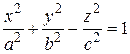 . (39)
. (39)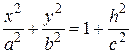 , z = h. (40)
, z = h. (40)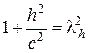 , видим, что кривая (40) есть эллипс
, видим, что кривая (40) есть эллипс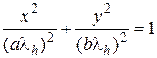 , z = h.
, z = h.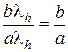
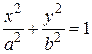 , z = 0,
, z = 0, .
. при |β| < b и
при |β| < b и 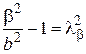 при |β| > b, видно, что эти кривые есть гиперболы:
при |β| > b, видно, что эти кривые есть гиперболы: и
и 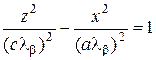 при y = β.
при y = β. , y = ± b;
, y = ± b;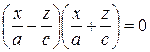 , y = ± b;
, y = ± b;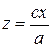 , y = ± b и
, y = ± b и  , y = ± b.
, y = ± b. , x = ± a и
, x = ± a и 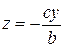 , x = ± a.
, x = ± a.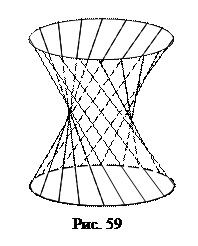
 ,
,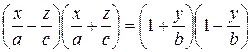 .
.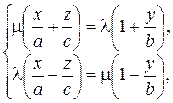 (41)
(41)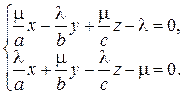
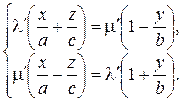 (42)
(42) (43)
(43) Для того, чтобы перейти от уравнения линии (43) к уравнению поверхности вращения, заменим х на
Для того, чтобы перейти от уравнения линии (43) к уравнению поверхности вращения, заменим х на 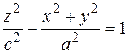 .
.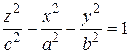 . (44)
. (44)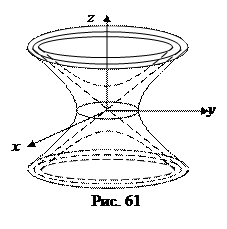 Асимптотический конус для двуполостного гиперболоида определяется так же, как и для однополостного (рис. 61).
Асимптотический конус для двуполостного гиперболоида определяется так же, как и для однополостного (рис. 61).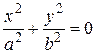 ,
,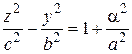 и
и 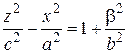 .
. называемую параболоидом вращения. Сжатие к плоскости у = 0 переводит параболоид вращения в поверхность с уравнением
называемую параболоидом вращения. Сжатие к плоскости у = 0 переводит параболоид вращения в поверхность с уравнением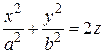 . (45)
. (45)
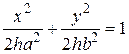
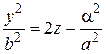 , x = α
, x = α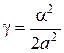 .
.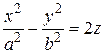 . (49)
. (49) Исследуем внешний вид гиперболического параболоида с помощью сечений (рис. 63). Сечение плоскостью z = h представляет собой гиперболу, которая в этой плоскости имеет уравнение:
Исследуем внешний вид гиперболического параболоида с помощью сечений (рис. 63). Сечение плоскостью z = h представляет собой гиперболу, которая в этой плоскости имеет уравнение: или
или  .
.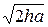 и
и 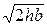 велики и уменьшаются с уменьшением h. При этом ось гиперболы, которая ее пересекает, параллельна вектору e 1.
велики и уменьшаются с уменьшением h. При этом ось гиперболы, которая ее пересекает, параллельна вектору e 1.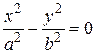 =>
=> 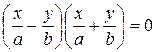
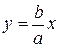 ,
, 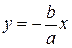 .
. ,
,  , x = α
, x = α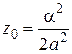 .
. Oz, а подвижная – «вниз».
Oz, а подвижная – «вниз». .
.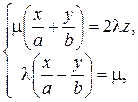 (53)
(53)