 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Директрисы эллипса и гиперболы
Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии a /ε от него, называют директрисами эллипса (здесь а – большая полуось, ε – эксцентриситет эллипса). Уравнения директрис эллипса, заданного каноническим уравнением (7), имеют вид
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a /ε от него, называются директрисами гиперболы (здесь а – действительная полуось, ε – эксцентриситет гиперболы). Уравнения директрис гиперболы, заданной каноническим уравнением (15), имеют вид
Так как для гиперболы ε > 1, то a /ε < a. Отсюда следует, что правая директриса расположена между центром и правой вершиной гиперболы, а левая – между центром и левой вершиной (рис. 46).
Теорема. Если r – расстояние от произвольной точки М эллипса до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d есть постоянная величина, равная эксцентриситету эллипса. Доказательство. Предположим для определенности, что речь идет о правом фокусе F 2 и правой директрисе. Пусть М (х; у) – произвольная точка эллипса (см. рис. 45). Расстояние от точки М до правой директрисы определяется равенством
которое легко устанавливается из рисунка. Из равенств (2) и (4) имеем r = r 2 = Полагая c / a = ε, получаем формулу расстояния от точки М до правого фокуса: r = a – ε x. (21) Из соотношений (20) и (21) находим
Теорема доказана. Теорема. Если r – расстояние от произвольной точки М гиперболы до какого-нибудь фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d есть величина постоянная, равная эксцентриситету гиперболы. Доказательство. Предположим для определенности, что речь идет о правом фокусе F 2 и правой директрисе. Пусть М (х; у) – произвольная точка гиперболы (см.рис. 46). Рассмотрим два случая. 1) Точка М находится на правой ветви гиперболы. Тогда расстояние от точки М до правой директрисы определяется равенством
которое легко устанавливается из рисунка. Из равенств (10) и (12) имеем r = r 2 = Полагая c / a = ε, получаем формулу расстояния от точки М до правого фокуса: r = ε x – a. (23) Из соотношений (22) и (23) находим
2) Точка М находится на левой ветви гиперболы. Тогда расстояние от точки М до правой директрисы определяется равенством
Из равенств (10) и (12) имеем r = r 1 = Полагая c / a = ε, получаем формулу расстояния от точки М до правого фокуса: r = –(ε x – a). (25) Из соотношений (24) и (25) находим
Теорема доказана. Установленное свойство эллипса и гиперболы можно положить в основу общего определения этих линий: множество точек, для которых отношение расстояний до фокуса и до соответствующий директрисы является величиной постоянной, равной ε, есть эллипс, если ε < 1, и гипербола, если ε > 1. Возникает вопрос, что представляет собой множество точек, определенное аналогичным образом при условии ε = 1. Оказывается, это новая линия второго порядка, называемая параболой.
Дата добавления: 2015-01-18 | Просмотры: 1275 | Нарушение авторских прав |
 и
и  .
. Так как для эллипса ε < 1, то a /ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины (рис. 45).
Так как для эллипса ε < 1, то a /ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая – левее его левой вершины (рис. 45). и
и  С помощью понятий директрисы и эксцентриситета можно сформулировать общее свойство, присущее эллипсу и гиперболе. Имеют место следующие две теоремы.
С помощью понятий директрисы и эксцентриситета можно сформулировать общее свойство, присущее эллипсу и гиперболе. Имеют место следующие две теоремы. , (20)
, (20)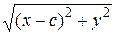 =
=  .
. .
. , (22)
, (22)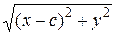 =
= 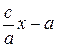 .
.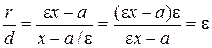 .
.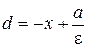 . (24)
. (24) =
= 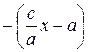 .
. .
.