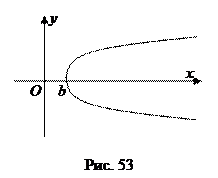|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Парабола
Определение. Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и на проходящей через фокус. Для вывода уравнения параболы введем на плоскости прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус перпендикулярно директрисе, и будем считать положительным направление от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой. Выведем уравнение параболы в выбранной системе координат.
r = d. (26) Чтобы получить искомое уравнение, нужно в равенстве (26) заменить переменные r и d их выражениями через координаты х и у. Фокус F имеет координаты (р /2;0); поэтому, используя формулу, выражающую расстояние между точками М и F, находим
Обозначим через Q основание перпендикуляра, опущенного из точки М на директрису. Очевидно, точка Q имеет координаты (– p /2; у). Тогда с помощью формулы, выражающей расстояние между точками М и Q, находим
Заменяя в равенстве (26) r и d выражениями (27) и (28), получим
Это и есть искомое уравнение параболы. Приведем его к более удобному виду, для чего возведем обе части равенства (29) в квадрат. Получаем x 2 – px + или y 2 = 2 px. (30) Проверим, что уравнение (30) после возведения в квадрат обеих частей равенства (29) не приобрело «лишних» корней. Для этого достаточно показать, что для любой точки, координаты х и у которой удовлетворяют уравнению (30), выполнено соотношение (26). Действительно, из уравнения (30) вытекает, что x ≥ 0, поэтому для точек, с неотрицательными абсциссами имеем d = p /2 + x. Подставляя значение y 2 из (30) в выражение (27) и учитывая, что x ≥ 0, получаем r = p /2 + x, т. е. величины r и d равны, что и требовалось доказать. Таким образом, уравнению (30) удовлетворяют координаты точек данной параболы и только они, т. е. это уравнение является уравнением данной параболы. Уравнение (30) называется каноническим уравнением параболы. Так как это уравнение второй степени, то парабола – линия второго порядка. Исследуем теперь форму параболы по ее каноническому уравнению. Так как уравнение (30) содержит у только в четной степени, то парабола симметрична относительно оси Оx. Следовательно, достаточно рассмотреть только ее часть, лежащую в верхней полуплоскости. Для этой части y > 0, поэтому, разрешая уравнение (30) относительно у, получаем
Из равенства (31) вытекают следующие утверждения: 1) если x < 0, то уравнение (31) дает мнимые значения у и, следовательно, левее оси Оy ни одной точки параболы нет; 2) если х = 0, то у = 0, т. е. начало координат лежит на параболе и является самой левой ее точкой; 3) при возрастании х возрастает и у, причем если x →+∞, то y →+∞.
Симметрично отражая рассмотренную часть параболы относительно оси Ox, получаем всю параболу (рис. 48), заданную уравнением (30). Точка О называется вершиной параболы, ось симметрии (ось Ox) – осью параболы. Число р, т. е. параметр пара
Уравнение x 2 = –2 py, p > 0 определяет параболу, лежащую ниже оси Ox, с вершиной в начале координат (рис. 51). Уравнение параболы, изображенной на рис. 52, имеет вид x 2 = 2 p (y – a), p > 0, a < 0, ее вершина смещена вниз на a.
y 2 = 2 p (x – b), p > 0, b > 0.
Пример. Дано уравнение параболы y 2 = 6 x. Составить уравнение ее директрисы и найти координаты ее фокуса. Решение. Сравнивая данное уравнение с каноническим уравнением параболы (30), заключаем, что 2 р = 6, откуда р = 3. Так как фокус параболы имеет координаты (р /2; 0), а директриса – уравнение х = – р /2, то для данной параболы получаем: координаты фокуса (3/2; 0) и уравнение директрисы х = –3/2.
Дата добавления: 2015-01-18 | Просмотры: 1632 | Нарушение авторских прав |
 Пусть М (х; у) – произвольная точка параболы. Обозначим через r расстояние от точки М до фокуса F (r = | FM |), через d – расстояние от точки М до директрисы, а через р – расстояние от фокуса до директрисы (рис. 47). Величину р называют параметром параболы, ее геометрический смысл будет раскрыт далее. Точка М будет лежать на данной параболе тогда и только тогда, когда
Пусть М (х; у) – произвольная точка параболы. Обозначим через r расстояние от точки М до фокуса F (r = | FM |), через d – расстояние от точки М до директрисы, а через р – расстояние от фокуса до директрисы (рис. 47). Величину р называют параметром параболы, ее геометрический смысл будет раскрыт далее. Точка М будет лежать на данной параболе тогда и только тогда, когда . (27)
. (27) . (28)
. (28)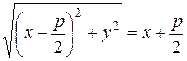 . (29)
. (29) + y 2 = x 2 + px +
+ y 2 = x 2 + px +  . (31)
. (31) Таким образом, переменная точка М (х; у), перемещаясь по параболе, исходит из начала координат и с ростом х движется «вправо» и «вверх», причем при x →+∞ точка М бесконечно удаляется как от оси Oy, так и от оси Ox.
Таким образом, переменная точка М (х; у), перемещаясь по параболе, исходит из начала координат и с ростом х движется «вправо» и «вверх», причем при x →+∞ точка М бесконечно удаляется как от оси Oy, так и от оси Ox. болы, как известно, выражает расстояние от фокуса до директрисы. Выясним, как влияет параметр параболы на ее форму. Для этого возьмем какое-нибудь определенное значение абсциссы, например х = 1, и из уравнения (30) найдем соответствующие значения ординаты:
болы, как известно, выражает расстояние от фокуса до директрисы. Выясним, как влияет параметр параболы на ее форму. Для этого возьмем какое-нибудь определенное значение абсциссы, например х = 1, и из уравнения (30) найдем соответствующие значения ординаты: 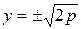 . Получаем на параболе две точки
. Получаем на параболе две точки 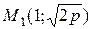 и
и  , симметричные относительно ее оси; расстояние между ними равно
, симметричные относительно ее оси; расстояние между ними равно  . Отсюда заключаем, что это расстояние тем больше, чем больше р. Следовательно параметр р характеризует «ширину» области, ограниченной параболой. В этом и состоит геометрический смысл параметра р.
. Отсюда заключаем, что это расстояние тем больше, чем больше р. Следовательно параметр р характеризует «ширину» области, ограниченной параболой. В этом и состоит геометрический смысл параметра р. Парабола, уравнение которой y 2 = –2 px, где p > 0, расположена слева от оси ординат (рис. 49). Вершина этой параболы совпадает с началом координат, осью симметрии является ось Ox.
Парабола, уравнение которой y 2 = –2 px, где p > 0, расположена слева от оси ординат (рис. 49). Вершина этой параболы совпадает с началом координат, осью симметрии является ось Ox. По аналогии с предыдущим можно утверждать, что уравнение x 2 = 2 py, p > 0 является уравнением параболы, вершина которой совпадает с началом координат, а осью симметрии является ось Oy (рис. 50). Эта парабола лежит выше оси абсцисс.
По аналогии с предыдущим можно утверждать, что уравнение x 2 = 2 py, p > 0 является уравнением параболы, вершина которой совпадает с началом координат, а осью симметрии является ось Oy (рис. 50). Эта парабола лежит выше оси абсцисс. Парабола, изображенная на рис. 53, имеет вершину в точке (b; 0), ее уравнение имеет вид
Парабола, изображенная на рис. 53, имеет вершину в точке (b; 0), ее уравнение имеет вид