 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Примеры решения типовых задач. Напомним, что окружность является частным случаем эллипса
Напомним, что окружность является частным случаем эллипса. Если в уравнении эллипса
полуоси равны a 2 = b 2 = R 2, то уравнение примет вид:
умножая которое на R 2, получим x 2 + y 2 = R 2 – уравнение окружности с центром в начале координат и радиусом R. Если центр окружности в точке (α, β), то делая сдвиг начала координат в центр окружности, получаем уравнение (x – α)2 + (y – β)2 = R 2. Рассмотрим примеры задач на использование уравнения окружности. Пример 1. Написать уравнение окружности радиуса R = 6 с центром в точке N (2; –3). После подстановки α = 2, β = –3, R = 6 в уравнение окружности, получаем (x – 2)2 + (y – (–3))2 = 62 => (x – 2)2 + (y + 3)2 = 36. Пример 2. Найти координаты центра и радиуса окружности x 2 + y 2 – 6 x + 10 y – 15 = 0. Выделим в данном уравнении полные квадраты: (x 2 – 6 x + 9) – 9 + (y 2+ 10 y + 25) – 25 – 15 = 0, (x – 3)2 + (y + 5)2 = 49. Получили уравнение окружности с центром в точке с координатами (3; –5) и радиусом 7. Напомним, что числа a и b (а > 0, b > 0) из уравнения эллипса
называются большой и малой полуосью эллипса. Введя обозначение c 2 = a 2 – b 2, c > 0, получим координаты фокусов F 1(– с; 0), F 2(с; 0) и эксцентриситет эллипса Пример 3. Найти полуоси, фокусы и эксцентриситет эллипса 4 x 2 + 9 y 2 = 16. Разделив на 16 обе части уравнения, получим
Таким образом, a 2 = 4 => а = 2 и b 2 = 16/9 => b = 4/3. Найдем c 2: c 2 = a 2 – b 2 = 4 – 16/9 = 20/9 и, значит, c =
Пример 4. Написать каноническое уравнение эллипса, симметричного относительно координатных осей и проходящего через точки L ( Учитывая, что уравнение эллипса имеет вид
Следовательно, a 2 = 36. Найдем b 2:
Таким образом, искомое уравнение будет
Перейдем к рассмотрению гиперболы. Пример 5. Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы 9 x 2 – 16 y 2 = 144. Приведем данное уравнение к каноническому виду, для чего необходимо разделить обе его части на 144, получим:
Таким образом, a 2 = 16, b 2 = 9 и а = 4 – действительная полуось, b = 3 – мнимая. Следовательно, c 2 = a 2 + b 2 = 16 + 9 = 25 и координаты фокусов: F 1(–5; 0), F 2(5; 0). Эксцентриситет Аналогично, учитывая что директрисы гиперболы определяются как и директрисы эллипса Пример 6. Составить каноническое уравнение гиперболы, симметричной относительно координатных осей, пересекающих ось Oy и проходящей через две точки М (24; По условию задачи искомая гипербола пересекает ось Oy, поэтому ее уравнение ищем в виде
Так как точки M и N лежат на гиперболе, то их координаты удовлетворяют уравнению гиперболы. Подставим координаты данных точек в это уравнение
Из второго уравнения следует b 2 = 25, и, значит первое уравнение принимает вид
Уравнение гиперболы приобретает вид:
Учитывая, что c 2 = a 2 + b 2, найдем с: c 2 = 25 + 144 = 169 => с = 13. Фокусы данной гиперболы лежат на оси Oy и F 1(0; –13), F 2(0; 13). Перейдем к рассмотрению параболы. Пример 7. Найти координаты фокуса и уравнение директрисы параболы y 2 = 12 x. Определить расстояние от точки М (3; 6) до фокуса. Сравнивая каноническое уравнение параболы y 2 = 2 px с уравнением y 2 = 12 x, получаем 2 p = 12 и р = 6. Следовательно, уравнение директрисы
Пример 8. Составить уравнение геометрического места точек, одинаково удаленных от точки F (0; 3) и прямой у = –5. Определить точки пересечения этой кривой с осями координат. Пусть М (х; у) – произвольная точка геометрического места (рис. 65). По условию | FM | = | NM |, где N – основание перпендикуляра, опущенного из точки М на прямую у = –5.Так как
то x 2 + y 2 – 6 y + 9 = y 2 + 10 y + 25. Приводя подобные члены, получим уравнение x 2 = 16 y + 16 или x 2 = 16(y + 1). Это уравнение параболы с вершиной в точке А (0; –1), симметричной относительно оси Oy. Заданные в условии точка и прямая являются соответственно ее фокусом и директрисой. Для определения точек пересечения с осью Ox необходимо решить систему уравнений:
Получаем х = 4 и х = –4. Таком образом, M 1(–4; 0), M 2(4; 0) – две точки пересечения с осью Ox. Полагая в уравнении параболы х = 0, получаем точку M 3(0; –1) – точку пресечения параболы с осью Oy. Рассмотрим еще один пример на определение геометрического места точек. Пример 9. Составить уравнение линии, расстояние от каждой точки которой до точки А (2; 0) относится к ее расстоянию до прямой 5 x + 8 = 0 как 5:4. Пусть М (х; у) – произвольная точка данной линии, N – основание перпендикуляра, проведенного через точку М к прямой 5 x + 8 = 0, или x = –8/5. Расстояние от точки М до точки А и прямой x = –8/5 определяется соответственно формулами
По условию задачи
Откуда 16((x – 2)2 + y 2) = 25(x + 8/5)2, 16(x 2 – 4 x + 4 + y 2) = 25(x 2 + 16/5 x + 64/25), Раскроем скобки и приведем подобные слагаемые: 16 x 2 – 64 x + 64 + 16 y 2 = 25 x 2 + 80 x + 64, 9 x 2 – 16 y 2 + 144 x = 0. Выделим полные квадраты в левой части полученного уравнения: 9(x 2 + 16 x + 64) – 16 y 2 – 9 ∙ 64 = 0, 9(x + 8)2 – 16 y 2 = 9 ∙ 64,
Полученное уравнение – уравнение гиперболы с центром в точке С (–8; 0) и полуосями а = 8, b = 6. Рассмотрим поверхности второго порядка. Пример 10. Привести к каноническому виду уравнение 4 x 2 + 9 y 2 + 36 z 2 – 8 x – 18 y – 72 z + 13 = 0. Сгруппируем слагаемые с одинаковыми переменными: 4(x 2 – 2 x) +9(y 2 – 2 y) + 36(z 2 – 2 z) + 13 = 0. Дополним каждую из скобок до полного квадрата: 4(x 2 – 2 x + 1) – 4 +9(y 2 – 2 y + 1) – 9 + 36(z 2 – 2 z + 1) – 36 + 13 = 0, 4(x – 1)2 +9(y – 1)2 + 36(z – 1)2 = 36. Делим полученное уравнение на 36, получаем
Произведем параллельный перенос осей координат, приняв за новое начало координат точку O ′(1; 1; 1). Формулы преобразования координат имеют вид: x = x ′ + 1, y = y ′ + 1, z = z ′ + 1. Тогда уравнение поверхности примет вид:
Это уравнение эллипсоида с центром в точке O ′(1; 1; 1) и полуосями 3, 2 и 1 соответственно. Пример 11. Привести к каноническому виду уравнение x 2 – y 2 – 4 x + 8 y – 2 z = 0. Сгруппируем слагаемые, содержащие одинаковые переменные: (x 2 – 4 x) –(y 2 – 8 y) – 2 z = 0. Выделим полные квадраты: (x 2 – 4 x + 4) – 4 –(y 2 – 8 y + 16) + 16 – 2 z = 0, (x – 2)2 –(y – 4)2 – 2(z – 6) = 0. Введем обозначения x ′ = x – 2, y ′ = y – 4, z ′ = z – 6, перенеся начало координат в точку O ′(2; 4; 6). Уравнение поверхности будет иметь вид: x ′2 – y ′2 = 2 z ′. Это уравнение гиперболического параболоида.
Вопросы для самопроверки 1. Какие кривые второго порядка существуют? 2. Как определяется эллипс? 3. Что такое гипербола? 4. Что такое полуоси? 5. Каково геометрическое определение параболы? 6. Какая прямая называется директрисой? 7. Какие линии имеют фокус? 8. Какие поверхности называются поверхностями вращения? 9. Какие существуют поверхности второго порядка? 10. Какие поверхности второго порядка имеют прямолинейные образующие? Дата добавления: 2015-01-18 | Просмотры: 5800 | Нарушение авторских прав |
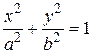
 ,
, .
. .
. . Следовательно, фокусы имеют следующие координаты: F 1(–
. Следовательно, фокусы имеют следующие координаты: F 1(–  ; 0), F 2(
; 0), F 2( ; 0). Найдем эксцентриситет:
; 0). Найдем эксцентриситет: .
. ;
;  и
и  .
. =>
=>  => b 2 = 16.
=> b 2 = 16. .
. .
. . Учитывая, что асимптоты гиперболы задаются уравнениями
. Учитывая, что асимптоты гиперболы задаются уравнениями  , получаем
, получаем  – уравнения асимптот.
– уравнения асимптот. , получаем
, получаем  .
. ), N (0; 5). Найти фокусы этой гиперболы.
), N (0; 5). Найти фокусы этой гиперболы. .
. и
и  .
. =>
=>  => a 2 = 122 = 144 и a = 12.
=> a 2 = 122 = 144 и a = 12. .
. = –3. Фокус находится в точке
= –3. Фокус находится в точке  , т. е. F (3; 0). Найдем расстояние от точки М (3; 6) до фокуса F (3; 0):
, т. е. F (3; 0). Найдем расстояние от точки М (3; 6) до фокуса F (3; 0):
 .
. и
и  ,
, , откуда получаем после возведения в квадрат
, откуда получаем после возведения в квадрат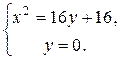
 ,
,  .
. :
:  = 5:4.
= 5:4. 5
5  .
. .
. .
.