 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Разностная аппроксимация задачи Дирихле для уравнения Пуассона
Рассмотрим уравнение Пуассона
Будем искать его решение, непрерывное в прямоугольнике
и принимающее на границе
Задача, определяемая уравнением (4.1) и условием (4.2), называется задачей Дирихле. Введем в
Чтобы написать разностную схему для задачи (4.1), (4.2), аппроксимируем каждую из производных
Пользуясь этими выражениями, заменим (4.1) разностным уравнением:
Граничные условия (4.2) заменим разностными функциями:
Точки
которое называется множеством внутренних точек сетки Совокупность точек Схема (4.3), (4.4) имеет второй порядок аппроксимации по Дата добавления: 2015-01-18 | Просмотры: 1112 | Нарушение авторских прав |
 (4.1)
(4.1)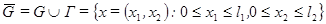
 заданные значения:
заданные значения: (4.2)
(4.2) прямоугольную сетку
прямоугольную сетку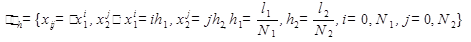 .
. и
и  на трехточечном шаблоне, полагая
на трехточечном шаблоне, полагая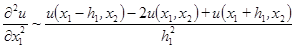 ,
,  .
. (4.3)
(4.3)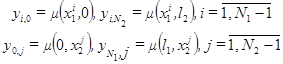 (4.4)
(4.4)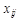 , в которых записываются уравнения (4.3), принадлежат подмножеству
, в которых записываются уравнения (4.3), принадлежат подмножеству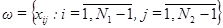 ,
,  ,
, .
.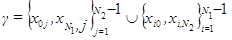 , в которых заданы разностные граничные условия (4.4), называются границей сетки
, в которых заданы разностные граничные условия (4.4), называются границей сетки  ,
,  ,
,  ,
,  не участвуют в данной аппроксимации и поэтому не относятся ни к внутренним, ни к граничным точкам.
не участвуют в данной аппроксимации и поэтому не относятся ни к внутренним, ни к граничным точкам.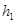 и
и  , и представляет собой систему линейных алгебраических уравнений относительно
, и представляет собой систему линейных алгебраических уравнений относительно 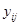 , состоящую из
, состоящую из 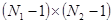 уравнений и стольких же неизвестных.
уравнений и стольких же неизвестных.