 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 2.3 Неявные схемы
Разностная схема, использующая этот шаблон имеет вид:
Здесь Схема имеет первый порядок аппроксимации по t и второй по h. Решение системы (2.10) находится по слоям начиная с n = 1. Для нахождения
где Эту систему можно решать методом прогонки. Схема (2.10) абсолютно устойчива.
Разностная схема, использующая этот шаблон имеет вид:
Если Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему:
При Исследуем погрешность аппроксимации схемы (2.13) на решении исходной задачи (2.1)-(2.3). Представим решение задачи (2.13) в виде
Входящая в правую часть уравнения (2.14) сеточная функция
называется погрешность аппроксимации схемы (2.13) на решении задачи (2.1)-(2.3). Разложим все функции, входящие в выражение для
где получим
Отсюда проводя разложения в точке
и, перегруппировывая слагаемые, получим, что
Учитывая уравнение (2.1)
Из формулы (2.15) можно сделать следующие выводы. Если Если При остальных значениях s и при Все схемы вида (2.13) с
где Система (2.16) решается методом прогонки. Условия устойчивости прогонки при
и выполнены при Дата добавления: 2015-01-18 | Просмотры: 1050 | Нарушение авторских прав |
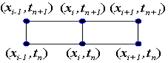
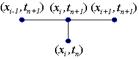 Для построения чисто неявной схемы для уравнения теплопроводности (схемы с опережением) зададим шаблон, состоящий из четырех узлов:
Для построения чисто неявной схемы для уравнения теплопроводности (схемы с опережением) зададим шаблон, состоящий из четырех узлов: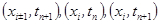 .
.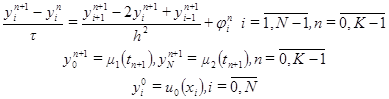 (2.10)
(2.10)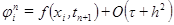 .
.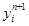 по известным
по известным 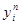 требуется решить систему уравнений:
требуется решить систему уравнений: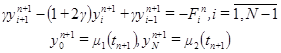 , (2.11)
, (2.11)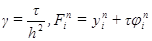 .
. Для построения шеститочечной симметричной схемы
Для построения шеститочечной симметричной схемы 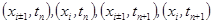 .
.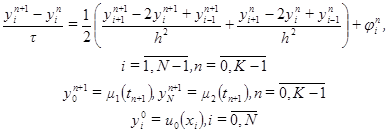 (2.12)
(2.12)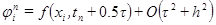 , то схема (2.12) имеет второй порядок аппроксимации как по h, так и по t. Она абсолютно устойчива, и ее можно решать методом прогонки.
, то схема (2.12) имеет второй порядок аппроксимации как по h, так и по t. Она абсолютно устойчива, и ее можно решать методом прогонки.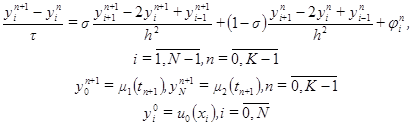 (2.13)
(2.13)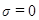 получим явную схему,
получим явную схему, 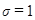 - чисто неявную схему,
- чисто неявную схему, 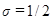 - симметричную схему.
- симметричную схему.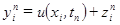 , где
, где 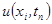 - точное решение дифференциальной задачи (2.1)-(2.3). Тогда для погрешности получим систему уравнений:
- точное решение дифференциальной задачи (2.1)-(2.3). Тогда для погрешности получим систему уравнений: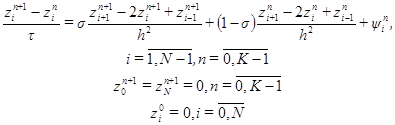 (2.14)
(2.14)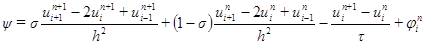
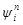 , по формуле Тейлора в точке
, по формуле Тейлора в точке 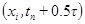 . Учитывая разложения
. Учитывая разложения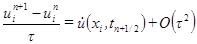 ,
, 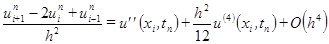 ,
,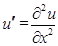 ,
, 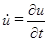 ,
, 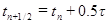 ,
,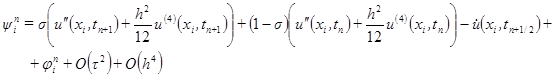 .
.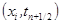 и обозначая
и обозначая 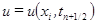 , будем иметь
, будем иметь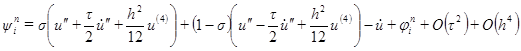 ,
,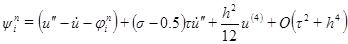 .
.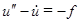 и следствие из него
и следствие из него 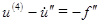 , окончательно можем записать, что
, окончательно можем записать, что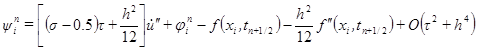 (2.15)
(2.15)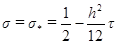 ,
, 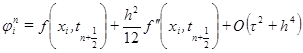 , то схема (2.13) имеет второй порядок аппроксимации по t и четвертыйпо h. Такая схема называется схемой повышенного порядка аппроксимации.
, то схема (2.13) имеет второй порядок аппроксимации по t и четвертыйпо h. Такая схема называется схемой повышенного порядка аппроксимации.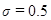 ,
, 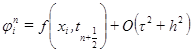 , то схема (2.13) имеет второй порядок аппроксимации по t и по h.
, то схема (2.13) имеет второй порядок аппроксимации по t и по h.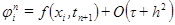 схема (2.13) имеет первый порядок аппроксимации по t и второй по h.
схема (2.13) имеет первый порядок аппроксимации по t и второй по h.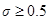 абсолютно устойчивы. При
абсолютно устойчивы. При 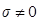 разностная схема (2.13) является неявной схемой. Для нахождения решения
разностная схема (2.13) является неявной схемой. Для нахождения решения 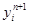 требуется решать систему уравнений
требуется решать систему уравнений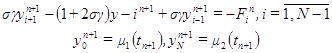 (2.16)
(2.16)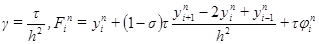 .
.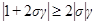
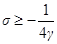 .
.