 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 2.2 Явная схемаДля построения разностной схемы введем сетку в области изменения независимых переменных. Сетку по x с шагом h обозначим Точки
Определение 2.2 Слоем называется множество всех узлов сетки Так, n-ым слоем называется множество узлов Так же для построения разностной схемы необходимо задать шаблон.
Чтобы аппроксимировать уравнение (2.1) в точке Производную
В результате получим разностное уравнение
Оно аппроксимирует исходное дифференциальное уравнение в точке Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные условия (начальные и граничные) - в граничных узлах сетки. Для уравнения теплопроводности (2.1), удовлетворяющего начальным условиям (2.2) и граничным условиям (2.3), разностная схема будет иметь вид:
Эта схема представляет собой систему линейных алгебраических уравнений с числом уравнений, равных числу неизвестных. Находить решение такой системы следует по слоям. Решение на нулевом слое задано начальными условиями (2.7). Если решение
а значения Погрешность аппроксимации
т.е. схему (2.5)-(2.7) можно применять только при условии (2.9).
Дата добавления: 2015-01-18 | Просмотры: 636 | Нарушение авторских прав |
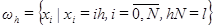 , сетку по t с шагом t обозначим
, сетку по t с шагом t обозначим 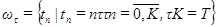 .
.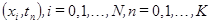 образуют узлы пространственно-временной сетки
образуют узлы пространственно-временной сетки 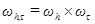 .
.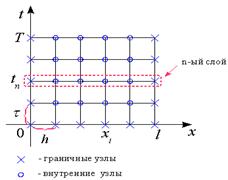 Определение 2.1 Узлы
Определение 2.1 Узлы 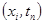 , принадлежащие отрезкам
, принадлежащие отрезкам 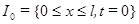 ,
, 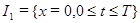 ,
, 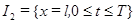 называются граничными узлами сетки
называются граничными узлами сетки 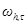 , а остальные узлы внутренними.
, а остальные узлы внутренними.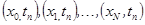 .
.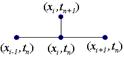 Определение 2.3 Шаблоном называется множество точек сетки, участвующих в аппроксимации дифференциального уравнения.
Определение 2.3 Шаблоном называется множество точек сетки, участвующих в аппроксимации дифференциального уравнения.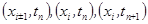 .
.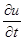 заменим в точке
заменим в точке 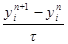 . Производную
. Производную 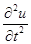 второй разностной производной
второй разностной производной 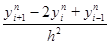 . Правую часть
. Правую часть 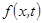 заменим приближенно сеточной функцией
заменим приближенно сеточной функцией 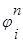 . В качестве
. В качестве 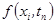 ,
, 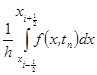 ,
, 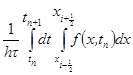 .
.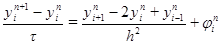 (2.4)
(2.4)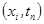 с первым порядком по h при условии, что разность
с первым порядком по h при условии, что разность 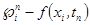 имеет тот же порядок малости.
имеет тот же порядок малости.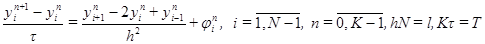 (2.5)
(2.5)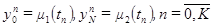 (2.6)
(2.6)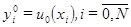 (2.7)
(2.7)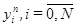 на слое n уже найдено, то решение
на слое n уже найдено, то решение 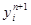 на слое n +1 находиться по явной формуле
на слое n +1 находиться по явной формуле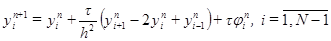 (2.8)
(2.8)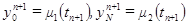 доопределяются из граничных условий. Поэтому схема (2.5)-(2.7) называется явной схемой.
доопределяются из граничных условий. Поэтому схема (2.5)-(2.7) называется явной схемой.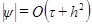 . Разностная схема устойчива при
. Разностная схема устойчива при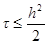 , (2.9)
, (2.9)