 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Глава 4. Разностные методы решения задач математической физики1 Определите понятие двойственности. 2 По каким правилам строится двойственная задача? 3 Сформулируйте основную теорему двойственности. 4 Сформулируйте следствие из основной теоремы двойственности. 5 Если ОДП одной из сопряженных задач пуста, какие выводы можно сделать о другой задаче? 6 Как получить решения двойственной задачи из решения исходной задачи симплекс-методом? 7 Сформулируйте теорему о равновесии. 8 Сформулируйте следствие из теоремы о равновесии. 9 Может ли двойственная оценка быть равной нулю, если соответствующее ограничение исходной задачи выполняется, как равенство? 10 В чем заключается экономическая интерпретация теоремы о равновесии? 11 Сформулируйте теорему об оценке. 12 Что такое теневая цена? 13 Что такое сокращенные затраты? 14 В чем заключается понятие устойчивости двойственных оценок? 15 В чем заключается понятие постоптимизационного анализа? 16 Нельзя ли сделать некоторые выводы (и какие) о решении двойственной задачи, если известно, что оптимальный план исходной задачи - вырожденный? 17 Построить и решить задачу, двойственную задаче 11 в разделе 3.4 (пример 3). 18 Построить задачу, двойственную задаче 11 в разделе 3.4 (пример 1), решить ее симплекс-методом и извлечь из заключительной симплексной таблицы решение прямой задачи. 19 Извлечь из решения задачи 11 (раздел 3.4, пример 1) решение двойственной задачи; проверить полученное решение с точки зрения теоремы о равновесии; провести анализ устойчивости двойственных оценок и проверить его результаты. 20 Построить и решить задачу, двойственную задаче 12 в разделе 3.4, решить ее симплекс-методом и извлечь из заключительной симплексной таблицы решение прямой задачи. 21 Извлечь из решения задачи 12 (раздел 3.4) решение двойственной задачи; проверить полученное решение с точки зрения теоремы о равновесии; провести анализ устойчивости двойственных оценок и проверить его результаты. * Не следует путать переменные Y двойственной задачи ни с дополнительными, ни с искусственными переменными, которые в предыдущих разделах иногда обозначались той же буквой. *В любом случае, их значения вычисляют, исходя из коэффициентов критериального ограничения в оптимальной симплексной таблице для прямой задачи, которые находятся в тех столбцах, которые в исходной симплексной таблице были базисными. * Это следует из физического смысла производной (скорость изменения функции в точке). * В разделе 4.2 обозначения y1, y2 и y3 использовались для искусственных переменных при построении расширенной задачи. Поскольку при изучении теории двойственности значения этих переменных использоваться почти не будут, нет необходимости использовать другие буквы латинского алфавита (хотя можно это сделать). Тем не менее, сделаем замечание о том, что не следует путать двойственные переменные с искусственными переменными, которые использовались при решении прямой задачи методом искусственного базиса. * Если при выполнении студентами упражнений для решения двойственной задачи потребуется применить метод искусственного базиса, рекомендуется обозначить искусственные переменные z1, z2 и т.д. * В таблице 19 нет оптимального значения двойственной переменной у5. Это объясняется тем, что она соответствует уравнению прямой задачи, в котором, естественно, нет дополнительной переменной. Однако при решении задачи симплекс-методом в разделе 4.2 в это ограничение вводилась искусственная переменная (ей соответствовал последний столбец N в таблицах 17-19). Отметим, что таблице 19 соответствуют строки 31-37 электронной таблицы. После того, как расширенная задача была решена, все искусственные переменные были исключены из рассмотрения и соответствующие столбцы коэффициентов более не пересчитывались. Если пересчитать их по тем же формулам, что и остальные столбцы (для этого в таблицах 18 и 19 достаточно скопировать формулы в диапазоне К25:К37 на диапазон L25:N37), то в последнем столбце критериальной строки (в N37) коэффициент будет равен 4 (у5 = 4). * Чтобы вычислить по модулю правые части неравенств во второй системе, нет необходимости проводить расчеты вручную. Можно ввести в любую свободную ячейку, например, в ячейку Т32 формулу =D32/G32, которую затем скопировать на диапазон Т33:T36.
Глава 4. Разностные методы решения задач математической физики §1. Основные понятия теории разностных схем: Пусть задана исходная дифференциальная задача
где f(x) - заданная функция; L - линейный дифференциальный оператор. Предполагается, что дополнительные условия (типа начальных и граничных) учтены оператором L и правой частью f. В качестве простейшего примера задачи (1.1) можно рассмотреть первую краевую задачу:
В общем случае уравнение (1.1) может быть многомерным, существенным является требование линейности оператора L. Для построения разностной схемы прежде всего вводится сетка Определение 1.1 Сеткой В общем случае h – вектор, причем определена величина Определение 1.2 Функция, определенная в точках сетки После введения сетки
Эта система называется разностной схемой или разностным задачей. Решение разностной задачи будем обозначать y. Пусть решение u (x) задачи (1.1) принадлежит линейному нормированному пространству Для сравнения функций из разных пространств введем оператор, сопоставляющий каждой функции из Потребуем, чтобы нормы в
Требование согласования норм обеспечивает единственность предела сеточных функций при
и
Пусть Определение 1.3 Сеточная функция Подставим
где
Определение 1.4 Сеточная функция Преобразуем выражение (1.1). Проецируя уравнение (1.1) на сетку
или, учитывая принятые обозначения
Из (1.5) и (1.6) получаем
т.е. где
Определение 1.5 Функции Определение 1.6 Говорят, что разностная задача (1.2) аппроксимирует исходную задачу (1.1), если
Аналогично определяются погрешность аппроксимации и порядок погрешности аппроксимации правых частей и дифференциального оператора. Введем понятие корректности разностной задачи: Определение 1.7 Разностная схема (1.2) называется корректной, если 1) ее решение существует и единственно при любых правых частях 2) существует постоянная
Свойство 2), означающее непрерывную зависимость, равномерную относительно h, решения разностной задачи от правой части, называется устойчивостью разностной схемы. Сформулируем понятие сходимости Определение 1.8 Решение разностной задачи (1.2) сходится к решению дифференциальной задачи (1.1), если при Справедлива следующая теорема о связи устойчивости и сходимости: Теорема 1.1 Пусть дифференциальная задача (1.1) поставлена корректно, разностная схема (1.2) является корректной и аппроксимирует исходную задачу (1.1). Тогда решение разностной задачи (1.2) сходится к решению исходной задачи (1.1), причем порядок точности совпадает с порядком аппроксимации. Дата добавления: 2015-01-18 | Просмотры: 1413 | Нарушение авторских прав |
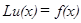 (1.1)
(1.1)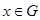 , G – область m -мерного пространства;
, G – область m -мерного пространства;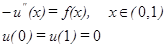
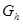 .
.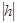 - длина вектора h. Обычно сетка
- длина вектора h. Обычно сетка 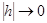 множество
множество 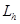 , правую часть f(x) – сеточной функцией
, правую часть f(x) – сеточной функцией 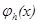 . В результате получим систему разностных уравнений
. В результате получим систему разностных уравнений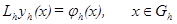 (1.2)
(1.2)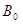 ,
, 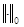 норма в
норма в 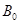 . Пусть сеточные функции
. Пусть сеточные функции 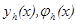 являются элементами линейного нормированного пространства
являются элементами линейного нормированного пространства 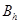 (пространство сеточных функций) с нормой
(пространство сеточных функций) с нормой 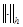 . По существу, имеем семейство линейных нормированных пространств, зависящих от параметра h.
. По существу, имеем семейство линейных нормированных пространств, зависящих от параметра h.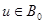 будем обозначать через
будем обозначать через 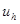 ее проекцию на пространство
ее проекцию на пространство 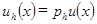 .
.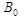 , т. е. чтобы для
, т. е. чтобы для 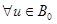 выполнялось условие
выполнялось условие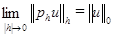 (1.3)
(1.3)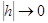 . Действительно, если для
. Действительно, если для 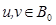 имеем
имеем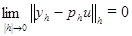 ,
, 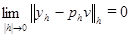 , то согласно (1.3)
, то согласно (1.3)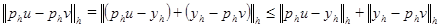
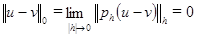 , т.е. u = v.
, т.е. u = v.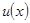 - решение исходной задачи (1.1),
- решение исходной задачи (1.1), 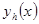 - решение разностной задачи (1.2).
- решение разностной задачи (1.2).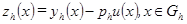 называется погрешностью разностной схемы (1.2).
называется погрешностью разностной схемы (1.2).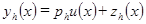 в уравнение (1.2). Тогда получим, что погрешность
в уравнение (1.2). Тогда получим, что погрешность 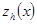 удовлетворяет уравнению
удовлетворяет уравнению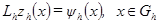 , (1.4)
, (1.4)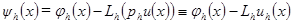 (1.5)
(1.5)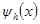 , определенная формулой (1.5), называется погрешностью аппроксимации разностной задачи (1.2) на решении исходной дифференциальной задачи (1.1).
, определенная формулой (1.5), называется погрешностью аппроксимации разностной задачи (1.2) на решении исходной дифференциальной задачи (1.1).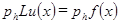
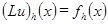 (1.6)
(1.6)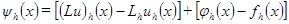 ,
,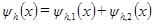 ,
,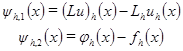 , (1.7)
, (1.7)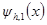 и
и 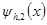 называются, соответственно, погрешностью аппроксимации дифференциального оператора L разностным оператором
называются, соответственно, погрешностью аппроксимации дифференциального оператора L разностным оператором 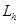 и погрешностью аппроксимации правой части.
и погрешностью аппроксимации правой части.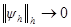 при
при 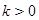 ,
, 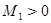 , независящие от h и такие, что
, независящие от h и такие, что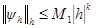
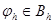 ;
;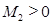 , не зависящая от h и такая, что при любых
, не зависящая от h и такая, что при любых 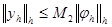 (1.8)
(1.8)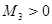 , независящие от h и такие, что
, независящие от h и такие, что 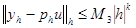 .
.