 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Трехслойные разностные схемы для уравнения колебанийРассмотрим первую краевую задачу для уравнения колебаний:
Задача поставлена корректно, т.е. ее решение существует и непрерывно зависит от начальных и граничных данных. Введем сетку
Минимальный шаблон, на котором можно аппроксимировать уравнение (3.1), это пятиточечный шаблон "крест". Таким образом, здесь требуется использовать три временных слоя: n -1, n, n +1. Такие схемы называются трехслойными.
Разностное уравнение (3.4) имеет второй порядок погрешности аппроксимации по t и по h. Решение
Для начала счета по формулам (3.6) должны быть заданы значения
Поскольку уравнение (3.4) аппроксимирует основное уравнение (3.1) со вторым порядком по, желательно, чтобы и разностное начальное условие также имело второй порядок аппроксимации. Чтобы добиться этого, воспользуемся разложением
учтем, что в силу дифференциального уравнения (3.1) выполняется равенство
Таким образом,
аппроксимирует второе из начальных условий (3.3) со вторым порядком по t и по h. Совокупность уравнений (3.4), (3.5), (3.7), (3.8) составляет разностную схему, аппроксимирующую задачу (3.1)-(3.3). Данная схема устойчива, если
Дата добавления: 2015-01-18 | Просмотры: 1473 | Нарушение авторских прав |
 (3.1)
(3.1)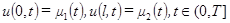 (3.2)
(3.2)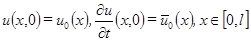 (3.3)
(3.3)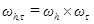 , где
, где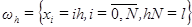 ,
, 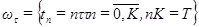 .
.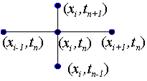 Простейшей разностной аппроксимацией уравнения (3.1) и граничных условий (3.2) является следующая система уравнений:
Простейшей разностной аппроксимацией уравнения (3.1) и граничных условий (3.2) является следующая система уравнений: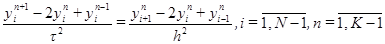 (3.4)
(3.4)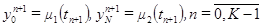 (3.5)
(3.5)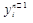 выражается явным образом через значения на предыдущих слоях.
выражается явным образом через значения на предыдущих слоях.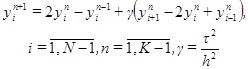 (3.6)
(3.6)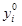 ,
, 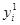 ,
,  . Из первого начального условия (3.3) сразу получаем
. Из первого начального условия (3.3) сразу получаем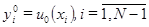 (3.7)
(3.7)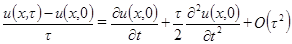 ,
,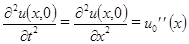
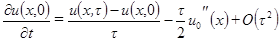 и, следовательно, разностное уравнение
и, следовательно, разностное уравнение (3.8)
(3.8)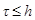 (3.9)
(3.9)