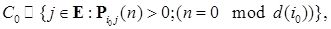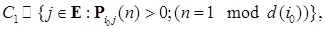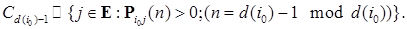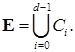|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Марковские цепи9.1. Пусть на стохастическом базисе Определение. Пусть Е - не более чем счетное множество (т. е. либо конечное, либо счетное), тогда марковская последовательность Обозначим через Обозначим Определение. Марковская цепь называется однородной, если Везде ниже будем рассматривать только однородные марковские цепи. Займемся теперь классификацией состояний. 9.2. Определение. Состояние Теорема 38. Если состояние Доказательство. Так как 9.2.1 Определение. Состояния Очевидно, что: 1) Определение. Говорят, что состояния Замечание. Класс - это множество состояний марковской цепи, являющихся сообщающимися. Через Теорема 39. Пусть два класса Доказательство теоремы 39. Пусть Замечания. 1) Теорема 39 полезна тем, что позволяет разбивать множество состояний 2) Если 9.2.2. Определение. Состояние Определение. Однородная марковская цепь называется неприводимой, если она состоит из одного класса сообщающихся состояний. Определение. Состояние Из этих определений очевидным образом следуют утверждения. Теорема 40. Пусть Теорема 41. Класс сообщающихся состояний состоит либо из существенных, либо из несущественных состояний. 9.3. В данном пункте мы определяем строго марковское свойство однородных марковских цепей, а также покажем, что однородная марковская цепь обладает строго марковскими свойством. Положим Используя эти обозначения для однородных марковских цепей
9.3.1. Определение. Будем говорить, что марковская цепь
где Теорема 42. Любая однородная марковская цепь обладает строго марковским свойством. Доказательство. Требуется установить (25), для этого достаточно установить равенство Действительно, для
Далее, так как
Отсюда в силу произвольности 9.4. Определение. Состояние 1) 2) Если Пусть
……………………………………………
Теорема 43. Если марковская цепь - неприводимая, то
Дата добавления: 2015-01-18 | Просмотры: 1078 | Нарушение авторских прав |
 задана марковская случайная последовательность
задана марковская случайная последовательность  со значениями в
со значениями в  и переходной вероятностью
и переходной вероятностью  .
. - одноточечное множество. Пусть B любое подмножество множества Е. Очевидно, что
- одноточечное множество. Пусть B любое подмножество множества Е. Очевидно, что  . Пусть
. Пусть 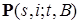 - переходная вероятность. Очевидно, что
- переходная вероятность. Очевидно, что  .
. - вероятность перехода последовательностью
- вероятность перехода последовательностью  в момент времени s в одноточечное множество
в момент времени s в одноточечное множество  в момент времени
в момент времени  .
. , т. е. переходная вероятность зависит только от разности
, т. е. переходная вероятность зависит только от разности  . Если
. Если  , то
, то 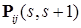 - переходная вероятность за один шаг, которую мы будем обозначать через
- переходная вероятность за один шаг, которую мы будем обозначать через  для однородных марковский цепей.
для однородных марковский цепей. за n шагов (обозначаем
за n шагов (обозначаем  ), если
), если  .
.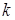 достижимо из
достижимо из  , то
, то  , то в силу соотношения Чепмена - Колмогорова, имеем
, то в силу соотношения Чепмена - Колмогорова, имеем 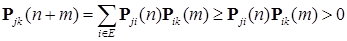 . Доказательство закончено.
. Доказательство закончено. и
и  ).
).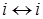 ; 2) если
; 2) если 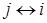 ; 3) если
; 3) если  , то
, то  .
. , если существуют моменты времени
, если существуют моменты времени  и
и  такие, что
такие, что  .
. обозначим класс состояний, которые сообщаются с состоянием
обозначим класс состояний, которые сообщаются с состоянием  , причем
, причем  и
и  . Тогда
. Тогда  .
. , следовательно существуют
, следовательно существуют  ,
,  такие, что
такие, что  . Из соотношения Чепмена - Колмогорова следует
. Из соотношения Чепмена - Колмогорова следует 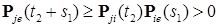 . Аналогично
. Аналогично  , следовательно
, следовательно  . Поэтому
. Поэтому  . Аналогично устанавливается
. Аналогично устанавливается  . Следовательно
. Следовательно  на классы
на классы  .
. .
. и
и  - однородная марковская цепь. Пусть
- однородная марковская цепь. Пусть  . Определим на
. Определим на  операторы сдвига
операторы сдвига  Для каждой
Для каждой  -измеримой случайной величины
-измеримой случайной величины  равенством определим случайную величину
равенством определим случайную величину 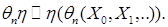
 - п. н. имеем
- п. н. имеем
 (24)
(24) обладает строго марковским свойством, если для любого марковского момента
обладает строго марковским свойством, если для любого марковского момента 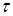
 , (25)
, (25) .
.
 , имеем
, имеем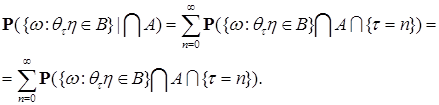 (26)
(26) , то имеем в силу марковского свойства,
, то имеем в силу марковского свойства,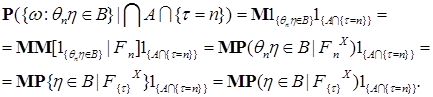
 и (26) получаем утверждение теоремы.
и (26) получаем утверждение теоремы. называется циклическим, а
называется циклическим, а  называется периодом марковской цепи если:
называется периодом марковской цепи если: , где
, где  (
( кратно
кратно  );
); , то такая марковская цепь называется апериодической.
, то такая марковская цепь называется апериодической.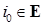 - фиксированное состояние. Введем подклассы:
- фиксированное состояние. Введем подклассы: