 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Эргодические марковские цепи11.1. Определение. Однородная марковская последовательность называется эргодической, если существует предел 1) Замечание. Эргодические процессы, в отличие от обычных марковских процессов, "не помнят" точку старта. Теорема 47 (достаточные условия существования эргодического распределения). Пусть Доказательство. Из соотношения Чепмена-Колмогорова, имеем
Обозначим: Аналогично устанавливается неравенство Из соотношения Чепмена - Колмогорова следует, что
Таким образом для
Аналогичным образом легко показать
Вычтем из (27) (28), имеем Доказательство закончено. 11.2. Теорема 48. Пусть имеется однородная марковская цепь 1) 2) 3) если 4) если Доказательство. 1) Пусть существует индекс
Мы пришли к противоречию. Значит наше предположение неверно, поэтому 2) Из утверждения 1) теоремы имеем
Устремляя в (29) 3) Если вектор 4) Доказательство закончено. Дата добавления: 2015-01-18 | Просмотры: 761 | Нарушение авторских прав |
 , который не зависит от состояния
, который не зависит от состояния  и выполняются условия:
и выполняются условия: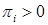 , 2)
, 2) 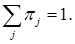
 - переходная вероятность за один шаг. Пусть существует
- переходная вероятность за один шаг. Пусть существует 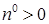 такое, что
такое, что  . Тогда существует вектор
. Тогда существует вектор 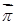 , компоненты которого
, компоненты которого  , причем для
, причем для 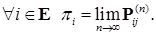
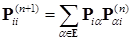 .
. Покажем, что
Покажем, что 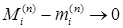 при
при 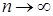 . Действительно
. Действительно 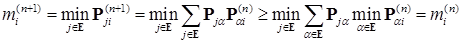 ,т. е.
,т. е. 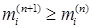 .
. .
.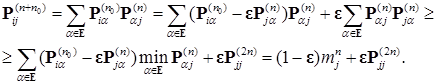
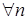 и
и  , имеем
, имеем 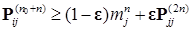 отсюда следует неравенство
отсюда следует неравенство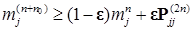 . (27)
. (27) (28)
(28)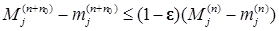 . Выбирая
. Выбирая  кратное
кратное 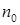 (например
(например 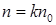 ), получаем, что
), получаем, что 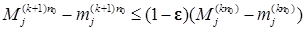 . Отсюда следует
. Отсюда следует 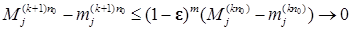 при
при  , а
, а 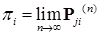 . Тогда
. Тогда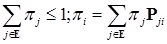 ;
;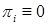 либо
либо 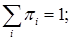
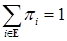 то эргодическое распределение существует и единственно.
то эргодическое распределение существует и единственно. .В силу леммы Фату
.В силу леммы Фату 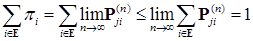 .Рассмотрим
.Рассмотрим 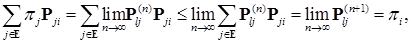 т. е.
т. е. 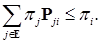
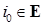 :
: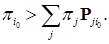 Следовательно
Следовательно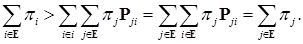
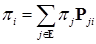 . (29)
. (29)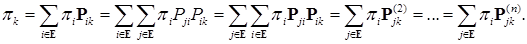
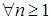
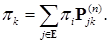
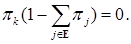
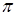 - распределение вероятностей.
- распределение вероятностей.