 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Классификация марковских цепей по асимптотическим свойствам10.1. Пусть
Очевидно, что Обозначим Предложение 44. Доказательство. Пусть
Заметим, что
Доказательство закончено. 10.2. Обозначим Определение. Состояние Определение. Теорема 45 (критерий возвратности). 1) Пусть имеется однородная марковская цепь (ОМЦ). Состояние 2) Если Доказательство. 1) Так как
Значит
Отсюда следует, что Утверждение ii) очевидным образом следует из i). Следствие 46. Если ряд Дата добавления: 2015-01-18 | Просмотры: 656 | Нарушение авторских прав |
 - марковская цепь. Обозначим
- марковская цепь. Обозначим  - марковский момент первого попадания в состояние
- марковский момент первого попадания в состояние  после момента времени
после момента времени  , т. е.
, т. е. 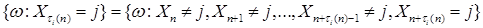 . Обозначим
. Обозначим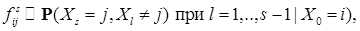
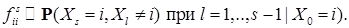
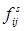 при
при 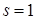 это переходная вероятность за один шаг из состояния
это переходная вероятность за один шаг из состояния  в
в  .
.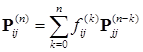
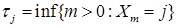 - момент первого попадания в состояние
- момент первого попадания в состояние 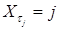 . Очевидно, что
. Очевидно, что 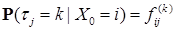 , так как
, так как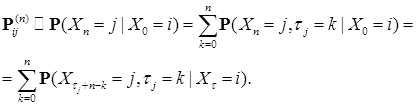
 , поэтому в силу строго марковского свойства, имеем
, поэтому в силу строго марковского свойства, имеем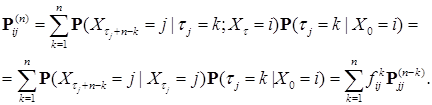
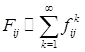 - вероятность того, что за бесконечное число шагов однородная марковская последовательность
- вероятность того, что за бесконечное число шагов однородная марковская последовательность  . Если
. Если 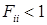 , то состояние называется невозвратным.
, то состояние называется невозвратным.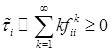 называется средним временем до возвращения в состояние
называется средним временем до возвращения в состояние  . Состояние
. Состояние 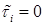 .
. .
.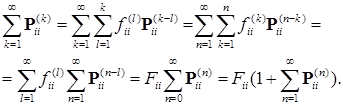
 .
.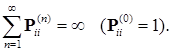
 сходится, то состояние
сходится, то состояние