Квадратично интегрируемые мартингалы
7.1. Определение. Пусть  мартингал относительно меры Р и мартингал относительно меры Р и  , тогда такой мартингал называется квадратично интегрируемым. , тогда такой мартингал называется квадратично интегрируемым.
Определение. Предсказуемая возрастающая последовательность, обозначаемая  , называется характеристикой квадратично интегрируемого мартингала , называется характеристикой квадратично интегрируемого мартингала  , если , если  - мартингал относительно меры Р. - мартингал относительно меры Р.
Теорема 28. Если  квадратично интегрируемый мартингал, то у него существует единственная характеристика квадратично интегрируемый мартингал, то у него существует единственная характеристика  , причем: , причем:
i)  Р - п. н., Р - п. н.,
ii)  - мартингал относительно меры Р. - мартингал относительно меры Р.
Доказательство. Существование и единственность характеристики квадратично интегрируемого мартингала  следует из теоремы Дуба-Мейера. Поэтому Р - п. н. справедливо представление следует из теоремы Дуба-Мейера. Поэтому Р - п. н. справедливо представление
 , ,
где  мартингал относительно меры Р. Отсюда следует, что Р - п. н. мартингал относительно меры Р. Отсюда следует, что Р - п. н.
 . (17) . (17)
Возьмем условное математическое ожидание  относительно левой и правой частей (17), имеем Р - п. н. относительно левой и правой частей (17), имеем Р - п. н.

Покажем, теперь, что 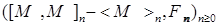 - мартингал. - мартингал.
Для этого достаточно показать, что  Р - п. н. Р - п. н.
Действительно, так как
 a a 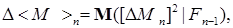 то то  . Доказательство закончено. . Доказательство закончено.
7.2. Определение. Пусть  и и  – квадратично интегрируемые мартингалы, предсказуемый случайный процесс, обозначаемый через – квадратично интегрируемые мартингалы, предсказуемый случайный процесс, обозначаемый через  , называется взаимной характеристикой квадратичноинтегрируемых мартингалов , называется взаимной характеристикой квадратичноинтегрируемых мартингалов  и и  , если , если  является мартингалом относительно фильтрации является мартингалом относительно фильтрации 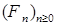 и меры Р. и меры Р.
Теорема 29. Если  и и  квадратично интегрируемые мартингалы, то взаимная характеристика квадратично интегрируемые мартингалы, то взаимная характеристика  существует и единственна, причем: существует и единственна, причем:
i) 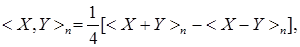
ii)  Р - п. н. Р - п. н.
Доказательство. Сначала заметим, что  и и  – квадратично интегрируемые мартингалы. Поэтому – квадратично интегрируемые мартингалы. Поэтому  и и  - являются мартингалами, причем - являются мартингалами, причем  и и  - единственные предсказуемые возрастающие процессы. Заметим, что - единственные предсказуемые возрастающие процессы. Заметим, что 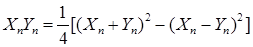 и поэтому и поэтому  является мартингалом относительно фильтрации является мартингалом относительно фильтрации 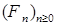 и меры Р. и меры Р.
Отсюда следует утверждение теоремы.
7.3. Определение. Пусть 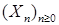 , ,  квадратично интегрируемые мартингалы относительно фильтрации квадратично интегрируемые мартингалы относительно фильтрации 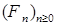 и меры Р. Будем говорить, что и меры Р. Будем говорить, что  и и  ортогональны, если ортогональны, если  является мартингалом. является мартингалом.
Теорема 30. Для того чтобы квадратично интегрируемые мартингалы  и и  были ортогональны, необходимо и достаточно, чтобы были ортогональны, необходимо и достаточно, чтобы 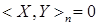 Р - п. н. для любого Р - п. н. для любого 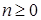 . .
Доказательство. Пусть  и и  ортогональны. В силу формулы Ито, имеем ортогональны. В силу формулы Ито, имеем
 (18) (18)
Заметим, что второе, третье и четвертое слагаемые правой части (18) являются мартингалами, поэтому  является мартингалом тогда и только тогда, когда является мартингалом тогда и только тогда, когда 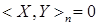 Р - п. н.. Р - п. н..
Следствие 31. Пусть  и и  квадратично интегрируемые мартингалы. Тогда квадратично интегрируемые мартингалы. Тогда  мартингал относительно меры Р. мартингал относительно меры Р.
Доказательство. Достаточно доказать, что  Р- п.н.. Действительно, Р- п.н.. Действительно,  , в силу теоремы 29, является мартингал-разностью. Доказательство закончено. , в силу теоремы 29, является мартингал-разностью. Доказательство закончено.
7.4. Теорема 32 (неравенство Куниты - Ватанабэ). Пусть  и и  квадратично интегрируемые мартингалы. Тогда Р - п. н. для любого квадратично интегрируемые мартингалы. Тогда Р - п. н. для любого 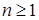
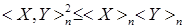
Доказательство следует из неравенства Коши и определения взаимной характеристики квадратично интегрируемого мартингала.
Теорема 33 (Разложение Куниты-Ватанабэ). Пусть  и и  -квадратично интегрируемые мартингалы относительно меры Р, принимающие значения в -квадратично интегрируемые мартингалы относительно меры Р, принимающие значения в  . .
Тогда существуют последовательности: i)  -предсказуемая; ii) -предсказуемая; ii)  мартингал относительно мер Р ортогональный мартингалу мартингал относительно мер Р ортогональный мартингалу  ; такие, что Р - п.н. справедливо разложение ; такие, что Р - п.н. справедливо разложение
 , (19) , (19)
причем разложение (19) –единственно.
Доказательство. Обозначим для любого 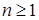 . .
 (20) (20)
Очевидно, что  - предсказуема. В силу того, что: - предсказуема. В силу того, что:
i)  -мартингал относительно меры Р; -мартингал относительно меры Р;
ii) из определения  следует, что следует, что 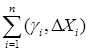 -мартингальное преобразование, а из неравенства Куниты-Ватанабэ следует, что оно является квадратично интегрируемым мартингалом относительно меры Р. -мартингальное преобразование, а из неравенства Куниты-Ватанабэ следует, что оно является квадратично интегрируемым мартингалом относительно меры Р.
Поэтому  - мартингал относительно меры Р. - мартингал относительно меры Р.
Покажем, что  - мартингал относительно меры Р. Для этого достаточно установить, в силу формулы Ито, равенство - мартингал относительно меры Р. Для этого достаточно установить, в силу формулы Ито, равенство
 Р - п.н., которое следует из (20). Отсюда вытекает, что Р - п.н., которое следует из (20). Отсюда вытекает, что  Р - п.н.. Следовательно, Р - п.н.. Следовательно, 
Установим единственность разложения (19). Действительно, пусть существуют  и и  относительно которых справедливо разложение (19). Тогда, если относительно которых справедливо разложение (19). Тогда, если  , то из (19) следует, что , то из (19) следует, что  - мартингал относительно потока - мартингал относительно потока  и меры Р. Поэтому и меры Р. Поэтому 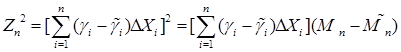 - мартингал. Следовательно, - мартингал. Следовательно, 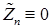 Р - п.н. Доказательство закончено. Р - п.н. Доказательство закончено.
7.5. Предложение 34. Пусть  - локальный мартингал относительно меры Р, а - локальный мартингал относительно меры Р, а 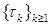 локализующая последовательность. Тогда локализующая последовательность. Тогда  для любого для любого  является квадратично интегрируемым мартингалом относительно меры Р. является квадратично интегрируемым мартингалом относительно меры Р.
Докажите самостоятельно.
Дата добавления: 2015-01-18 | Просмотры: 1151 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

 мартингал относительно меры Р и
мартингал относительно меры Р и  , тогда такой мартингал называется квадратично интегрируемым.
, тогда такой мартингал называется квадратично интегрируемым. , называется характеристикой квадратично интегрируемого мартингала
, называется характеристикой квадратично интегрируемого мартингала  - мартингал относительно меры Р.
- мартингал относительно меры Р. Р - п. н.,
Р - п. н., - мартингал относительно меры Р.
- мартингал относительно меры Р. ,
, мартингал относительно меры Р. Отсюда следует, что Р - п. н.
мартингал относительно меры Р. Отсюда следует, что Р - п. н. . (17)
. (17) относительно левой и правой частей (17), имеем Р - п. н.
относительно левой и правой частей (17), имеем Р - п. н.
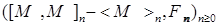 - мартингал.
- мартингал. Р - п. н.
Р - п. н. a
a 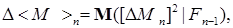 то
то  . Доказательство закончено.
. Доказательство закончено. и
и  – квадратично интегрируемые мартингалы, предсказуемый случайный процесс, обозначаемый через
– квадратично интегрируемые мартингалы, предсказуемый случайный процесс, обозначаемый через  , называется взаимной характеристикой квадратичноинтегрируемых мартингалов
, называется взаимной характеристикой квадратичноинтегрируемых мартингалов  является мартингалом относительно фильтрации
является мартингалом относительно фильтрации 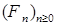 и меры Р.
и меры Р.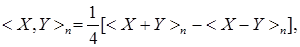
 Р - п. н.
Р - п. н. и
и  – квадратично интегрируемые мартингалы. Поэтому
– квадратично интегрируемые мартингалы. Поэтому  и
и  - являются мартингалами, причем
- являются мартингалами, причем  и
и  - единственные предсказуемые возрастающие процессы. Заметим, что
- единственные предсказуемые возрастающие процессы. Заметим, что 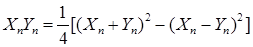 и поэтому
и поэтому  является мартингалом относительно фильтрации
является мартингалом относительно фильтрации 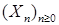 ,
,  квадратично интегрируемые мартингалы относительно фильтрации
квадратично интегрируемые мартингалы относительно фильтрации  является мартингалом.
является мартингалом.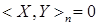 Р - п. н. для любого
Р - п. н. для любого 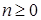 .
. (18)
(18) является мартингалом тогда и только тогда, когда
является мартингалом тогда и только тогда, когда  мартингал относительно меры Р.
мартингал относительно меры Р. Р- п.н.. Действительно,
Р- п.н.. Действительно,  , в силу теоремы 29, является мартингал-разностью. Доказательство закончено.
, в силу теоремы 29, является мартингал-разностью. Доказательство закончено.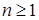
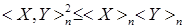
 .
. -предсказуемая; ii)
-предсказуемая; ii)  , (19)
, (19) (20)
(20) - предсказуема. В силу того, что:
- предсказуема. В силу того, что: следует, что
следует, что 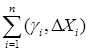 -мартингальное преобразование, а из неравенства Куниты-Ватанабэ следует, что оно является квадратично интегрируемым мартингалом относительно меры Р.
-мартингальное преобразование, а из неравенства Куниты-Ватанабэ следует, что оно является квадратично интегрируемым мартингалом относительно меры Р. - мартингал относительно меры Р.
- мартингал относительно меры Р. - мартингал относительно меры Р. Для этого достаточно установить, в силу формулы Ито, равенство
- мартингал относительно меры Р. Для этого достаточно установить, в силу формулы Ито, равенство Р - п.н., которое следует из (20). Отсюда вытекает, что
Р - п.н., которое следует из (20). Отсюда вытекает, что  Р - п.н.. Следовательно,
Р - п.н.. Следовательно, 
 и
и  относительно которых справедливо разложение (19). Тогда, если
относительно которых справедливо разложение (19). Тогда, если  , то из (19) следует, что
, то из (19) следует, что  - мартингал относительно потока
- мартингал относительно потока  и меры Р. Поэтому
и меры Р. Поэтому 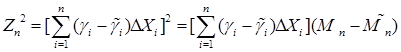 - мартингал. Следовательно,
- мартингал. Следовательно, 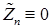 Р - п.н. Доказательство закончено.
Р - п.н. Доказательство закончено.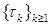 локализующая последовательность. Тогда
локализующая последовательность. Тогда  для любого
для любого  является квадратично интегрируемым мартингалом относительно меры Р.
является квадратично интегрируемым мартингалом относительно меры Р.