 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 3.2.2. Среднеквадратичное приближение
Рассмотрим как величину аппроксимации величину
Параметры Решение задачи о нахождении параметров Необходимые условия минимума функции
Если
где На практике часто используются функции
Тогда
многочлен степени
Таким образом, из (3.6) получаем систему следующего вида:
При Дата добавления: 2015-01-18 | Просмотры: 671 | Нарушение авторских прав |
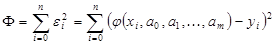 (3.5)
(3.5)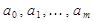 функции (3.1) будем искать таким образом, чтобы они минимизировали функцию
функции (3.1) будем искать таким образом, чтобы они минимизировали функцию 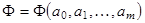 , определенную по формуле (3.5).
, определенную по формуле (3.5).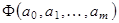 дают систему уравнений:
дают систему уравнений: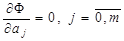 (3.6)
(3.6)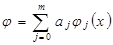 (3.7)
(3.7)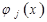 - линейно независимые функции, тогда система уравнений (3.6) будет линейной.
- линейно независимые функции, тогда система уравнений (3.6) будет линейной.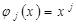 . (3.8)
. (3.8)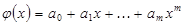 (3.9)
(3.9)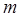 . Следовательно,
. Следовательно,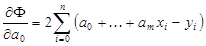
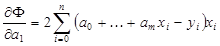
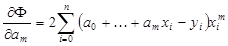
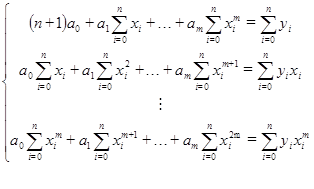 (3.10)
(3.10)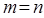 полученный многочлен совпадает с интерполяционным многочленом Лагранжа.
полученный многочлен совпадает с интерполяционным многочленом Лагранжа.