 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 1.1. Постановка задачи
Задача численного интегрирования состоит в нахождении приближенного значения интеграла
где На отрезке
где Определение 1.1. Приближенное равенство Задача численного интегрирования при помощи квадратур состоит в отыскании таких узлов При построении квадратурной формулы интеграл (1.1) обычно представляют в виде суммы интегралов по частичным отрезкам:
Для построения формулы численного интегрирования на всем отрезке
на частичном отрезке Дата добавления: 2015-01-18 | Просмотры: 753 | Нарушение авторских прав |
 , (1.1)
, (1.1) - заданная функция.
- заданная функция. вводится сетка
вводится сетка  . В качестве приближенного значения интеграла рассматривается число
. В качестве приближенного значения интеграла рассматривается число , (1.2)
, (1.2) - числовые коэффициенты.
- числовые коэффициенты. называется квадратурной формулой. Сумма
называется квадратурной формулой. Сумма  называется квадратурной суммой. Точки
называется квадратурной суммой. Точки  - узлами квадратурной формулы, числа
- узлами квадратурной формулы, числа  называется погрешностью квадратурной формулы.
называется погрешностью квадратурной формулы. и таких коэффициентов
и таких коэффициентов 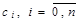 , чтобы погрешность квадратурной формулы была минимальной для функций из заданного класса.
, чтобы погрешность квадратурной формулы была минимальной для функций из заданного класса.  (1.3)
(1.3) (1.4)
(1.4) и воспользоваться свойством (1.3).
и воспользоваться свойством (1.3).