 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 2.2. Оценка погрешностиПолучим выражение для погрешности квадратурной формулы интерполяционного типа. Представим функцию
где
Тогда получим
Таким образом, погрешность
где Для погрешности интерполирования была получена формула
Отсюда приходим к следующей оценке погрешности квадратурной формулы интерполяционного типа:
где Из формулы (2.6) видно, что справедливо следующее утверждение: Утверждение 2.1. Квадратурная формула интерполяционного типа, построенная по (n +1) узлу
Справедливо и обратное утверждение: Утверждение 2.2. Если квадратурная формула Дата добавления: 2015-01-18 | Просмотры: 670 | Нарушение авторских прав |
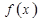 в виде
в виде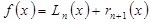 ,
,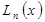 - интерполяционный многочлен для
- интерполяционный многочлен для 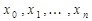 .
.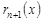 - погрешность интерполирования.
- погрешность интерполирования.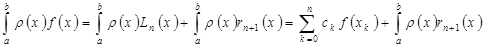
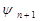 квадратурной формулы (2.2), (2.3) равна
квадратурной формулы (2.2), (2.3) равна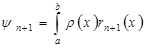 (2.4)
(2.4)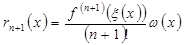 . Применив ее, получим
. Применив ее, получим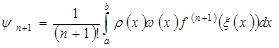 . (2.5)
. (2.5)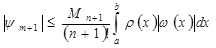 , (2.6)
, (2.6)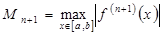 .
. - коэффициенты, вычисленные согласно (2.3), то имеет место равенство
- коэффициенты, вычисленные согласно (2.3), то имеет место равенство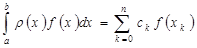 . (2.7)
. (2.7)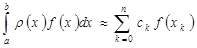 точна для любого многочлена степени n, то она является квадратурной формулой интерполяционного типа.
точна для любого многочлена степени n, то она является квадратурной формулой интерполяционного типа.