 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 2.2. Метод прогонкиРассмотрим систему линейных уравнений
Это система с трехдиагональной матрицей размерности
Для решения систем такого вида используется метод исключения неизвестных, называемый методом прогонки. Пусть имеет место соотношение
с неопределенными коэффициентами Подставим
Сравнивая это тождество с (2.16), находим
Из (2.16) при
Зная
Т.о., решение системы (2.13) –(2.15) методом прогонки, осуществляется по следующим формулам: Прямой ход:
Обратный ход:
Условия устойчивости метода прогонки:
Дата добавления: 2015-01-18 | Просмотры: 640 | Нарушение авторских прав |
 (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) :
: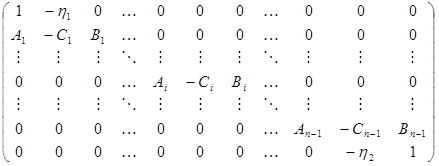
 (2.16)
(2.16)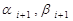
 в (2.13), получаем
в (2.13), получаем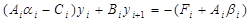
 (2.17)
(2.17) (2.18)
(2.18) и (2.14) получаем
и (2.14) получаем (2.19)
(2.19) и переходя от
и переходя от  к
к  в формулах (2.17) и (2.18) можно определить
в формулах (2.17) и (2.18) можно определить  для
для  . Вычисление по формуле (2.16) ведутся путем перехода от
. Вычисление по формуле (2.16) ведутся путем перехода от  можно найти
можно найти 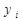 ) и для начала этих вычислений необходимо знать
) и для начала этих вычислений необходимо знать  . Определим
. Определим 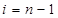
 (2.20)
(2.20)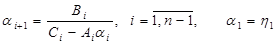
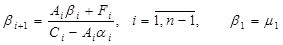
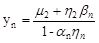
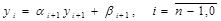
 ,
,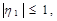

 .
.