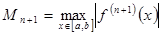|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 1.4. Погрешность интерполяционной формулыЗаменяя функцию Определение 1.6 Разность
называется погрешностью интерполирования, или остаточным членом интерполяционной формулы. В узлах интерполирования эта погрешность равна нулю. Оценим погрешность в любой точке
где
Пусть требуется оценить
Предположим, что Поскольку
получаем
Таким образом доказано, что погрешность интерполирования можно представить в виде
где Отсюда следует оценка
где Поскольку многочлены Лагранжа и Ньютона отличаются только формой записи, представление погрешности в виде (1.14) справедливо как для формулы Лагранжа, так и для формулы Ньютона. Дата добавления: 2015-01-18 | Просмотры: 816 | Нарушение авторских прав |
 интерполяционным многочленом
интерполяционным многочленом  , мы допускаем погрешность.
, мы допускаем погрешность.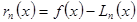
 . Для этого рассмотрим вспомогательную функцию
. Для этого рассмотрим вспомогательную функцию , (1.12)
, (1.12) ,
,  ,
, (1.13)
(1.13) в заданной точке
в заданной точке  из условия
из условия  . Для этого достаточно положить
. Для этого достаточно положить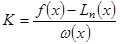
 имеет
имеет  непрерывную производную на отрезке
непрерывную производную на отрезке  . Функция
. Функция 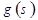 имеет не менее
имеет не менее  нулей на этом отрезке, а именно в точках
нулей на этом отрезке, а именно в точках  . Поэтому производная
. Поэтому производная  имеет не менее чем
имеет не менее чем  - не менее
- не менее 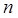 нулей и т.д., функция
нулей и т.д., функция  по крайней мере один раз обращается в нуль на
по крайней мере один раз обращается в нуль на  , в которой
, в которой  .
. ,
,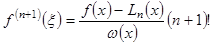 .
. (1.14)
(1.14) - многочлен, определенный согласно (1.13).
- многочлен, определенный согласно (1.13). (1.15)
(1.15)