 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 2.1. Вывод формулБудем рассматривать формулы приближенного вычисления интегралов
где
Рассматриваемые далее формулы имеют вид
где Квадратурные формулы будем получать путем замены интерполяционным многочленом сразу на всем отрезке Получим выражения для коэффициентов квадратурных формул интерполяционного типа. Пусть на
где Получим приближенную формулу вида (2.2), где
Таким образом, формула (2.2) является квадратурной формулой интерполяционного типа тогда и только тогда, когда ее коэффициенты вычисляются по правилу (2.3). Дата добавления: 2015-01-18 | Просмотры: 672 | Нарушение авторских прав |
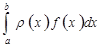 , (2.1)
, (2.1)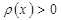 - заданная интерполируемая функция (так называемая весовая функция),
- заданная интерполируемая функция (так называемая весовая функция),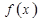 - достаточно гладкая функция.
- достаточно гладкая функция.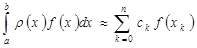 , (2.2)
, (2.2)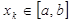 ,
,  - числовые коэффициенты,
- числовые коэффициенты, 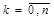 .
.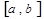 . Полученные таким образом формулы называются квадратурными формулами интерполяционного типа. Как правило, точность этих формул возрастает с увеличением числа узлов интерполирования. Формулы прямоугольников, трапеций и Симпсона являются частным случаем квадратурных формул интерполяционного типа, когда
. Полученные таким образом формулы называются квадратурными формулами интерполяционного типа. Как правило, точность этих формул возрастает с увеличением числа узлов интерполирования. Формулы прямоугольников, трапеций и Симпсона являются частным случаем квадратурных формул интерполяционного типа, когда 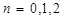 ,
, 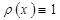 .
.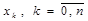 . Предполагается, что среди этих узлов нет совпадающих, в остальном они могут быть расположены как угодно на
. Предполагается, что среди этих узлов нет совпадающих, в остальном они могут быть расположены как угодно на 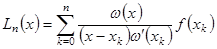 ,
,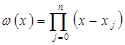 ,
, 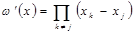 .
.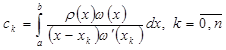 (2.3)
(2.3)