 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 2.1. Построение кубического сплайнаПусть на
Обозначим Определение 2.1 Интерполяционным кубическим сплайном, соответствующим данной функции 1. на каждом сегменте 2. функция 3.
На каждом из отрезков
поэтому
Из условия интерполирования
доопределим Из непрерывности функции
Обозначая перепишем это уравнение в следующем виде
Условия непрерывности первой производной
Условия непрерывности второй производной
Объединяя (2.4)-(2.6), получим систему Два недостающих уравнения получают, задавая те или иные граничные условия для
Условие
Исключая из этих уравнений переменные
Вычтем второе уравнение из первого, получаем
Подставим найденное выражение для Приведя подобные слагаемые, и умножив обе части уравнения на 2, получим
Рассмотрим два соседних уравнения вида (2.7) и умножим их на
Подставим эти выражения в (2.10), получаем
Окончательно для определения коэффициентов
Системы такого вида решаются методом прогонки. В силу диагонального преобладания система имеет единственное решение. По найденным коэффициентам ci коэффициенты bi, di определяются с помощью явных формул
Дата добавления: 2015-01-18 | Просмотры: 826 | Нарушение авторских прав |
 задана непрерывная функция
задана непрерывная функция  . Введем сетку
. Введем сетку .
. .
. называется функция
называется функция  , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям: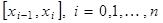 функция
функция 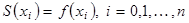 – выполняется условие интерполирования.
– выполняется условие интерполирования. в виде многочлена третьей степени:
в виде многочлена третьей степени: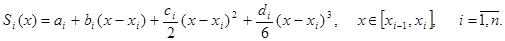 (2.1)
(2.1) – коэффициенты, подлежащие определению. Поясним смысл введенных переменных. Имеем
– коэффициенты, подлежащие определению. Поясним смысл введенных переменных. Имеем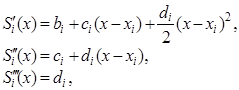
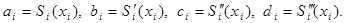
 , получаем
, получаем , (2.2)
, (2.2) .
.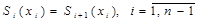 . Отсюда, учитывая выражение для
. Отсюда, учитывая выражение для  , получаем
, получаем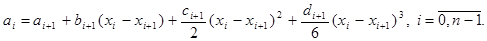
 (2.3)
(2.3) (2.4)
(2.4) приводят к уравнениям
приводят к уравнениям (2.5)
(2.5) приводят к уравнениям
приводят к уравнениям (2.6)
(2.6) уравнений относительно
уравнений относительно  неизвестных
неизвестных  ,
, 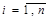 .
. , тогда естественно требовать, чтобы
, тогда естественно требовать, чтобы  . Отсюда получаем
. Отсюда получаем  , т.е.
, т.е.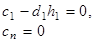
 совпадает с уравнением (2.6) при
совпадает с уравнением (2.6) при  , если положить
, если положить 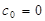 . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:
. Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна: (2.7)
(2.7) (2.8)
(2.8) (2.9)
(2.9) , получим систему, содержащую только
, получим систему, содержащую только  . Для этого рассмотрим два соседних уравнения вида (2.9):
. Для этого рассмотрим два соседних уравнения вида (2.9):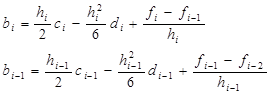
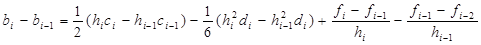
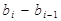 в правую часть уравнения (2.8), получим
в правую часть уравнения (2.8), получим  .
. (2.10)
(2.10) и
и  соответственно
соответственно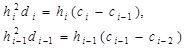
 .
. получаем систему уравнений
получаем систему уравнений (2.11)
(2.11) (2.12)
(2.12)