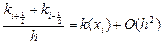|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.9.2. Построение трехточечной разностной схемы 2-го порядка аппроксимацииРассмотрим линейное дифференциальное уравнение второго порядка в самосопряженной форме
с краевыми условиями первого рода u (0)= μ 1, u (1)= μ 2 (9.4) Если Введем на отрезке [0,1] равномерную сетку
Запишем трехточечную разностную схему для краевой задачи (9.3)-(9.4) в прогоночном виде
Коэффициенты bi, ci, ai, φi зависят от значений функций k (x), q (x), f (x) в узлах сетки, а также от шага h. Перепишем разностную схему (9.5) в следующем виде:
где Схема называется однородной, если ее коэффициенты во всех узлах сетки для любого линейного дифференциального уравнения вычисляются по одним и тем же правилам. Для однородной схемы удобна система безиндексных обозначений:
Здесь a = a (x), b = b (x), d = d (x), y = y (x), x = ih, h Î wh
Найдем погрешность аппроксимации схемы (9.7)
По формуле Тейлора
тогда
Подставим выражения (*) в (9.8)
Т.о., схема (9.7) будет иметь 2-ой порядок аппроксимации, если будут выполняться следующие условия:
Эти условия выполняются, например, при где Действительно
поэтому
Дата добавления: 2015-01-18 | Просмотры: 1261 | Нарушение авторских прав |
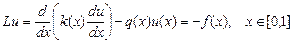 (9.3)
(9.3)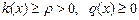 , то такая задача описывает стационарное распределение тепла в стержне. Задача имеет единственное решение, если k (x), q (x), f (x) –кусочно-непрерывные функции.
, то такая задача описывает стационарное распределение тепла в стержне. Задача имеет единственное решение, если k (x), q (x), f (x) –кусочно-непрерывные функции.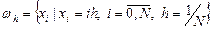
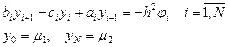 (9.5)
(9.5) (9.6)
(9.6)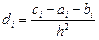 .
.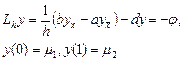 (9.7)
(9.7) ,
, 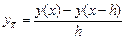
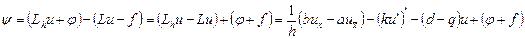 (9.8)
(9.8)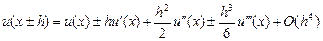
 (*)
(*)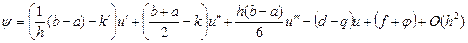
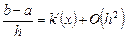 ,
,  , d = q(x)+O(h2), -j = f(x)+O(h2) (9.9)
, d = q(x)+O(h2), -j = f(x)+O(h2) (9.9) , (9.10)
, (9.10) ,
, 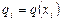 ,
,  .
. ,
,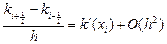 ,
,