 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.7.3. Нахождение решения неявной разностной схемыДвухточечная неявная схема Адамса (7.2) имеет вид нелинейного уравнения относительно неизвестного значения
где
Для решения уравнения (7.4) используется метод простой итерации:
Решение уравнения получается как предел последовательности состоящей из приближений
Это условие выполняется для достаточно малого h. Кроме того для работы метода (7.5)необходимо получить начальное приближение
Такое совместное использование экстраполяционной и интерполяционной разностных схем называется методом "предикатор-корректор". Вопрос о количестве итераций m, выполняемых на каждом шаге, решается по-разному. Иногда итерации произвдят до тех пор, пока не выполнится условие
при заданной точности ε. Чаще на каждом шаге выполняется фиксированное число m, как правило, небольшое. §8. Краевые задачи для ОДУ 2-го порядка. Рассмотрим краевую задачу для уравнения 2-го порядка, разрешенного относительно второй производной:
Будем искать решение
Граничные условия: Сущность метода стрельбы заключается в сведении краевой задачи (8.1)-(8.2) к решению последовательности задач Коши для того же уравнения (8.1) с начальными условиями
Здесь α – угол наклона касательной к интегральной кривой в этой точке. Считая решение задачи Коши
Уравнение (8.4) отличается от обычных уравнений тем, что функцию F (α) нельзя представить аналитическим выражением, она выражается через решение задачи Коши (8.1), (8.3). Однако для решения задачи (8.4) можно использовать рассмотренные ранее приближенные методы. Например, при использовании метода деления отрезка пополам поступаем следующим образом: Находим начальный отрезок
снова решаем задачу Коши при Название "метод стрельбы" связано с тем, что здесь как бы проводится "пристрелка" решения задачи Коши по углу наклона интегральной кривой в начальной точке отрезка. Этот алгоритм применим, если решение задачи Коши (8.1), (8.3) Для решения уравнения (8.4) используются и другие методы, например метод Ньютона
Т.к.
Дата добавления: 2015-01-18 | Просмотры: 732 | Нарушение авторских прав |
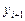 :
: , (7.4)
, (7.4)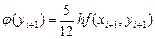 ,
,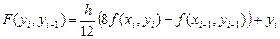
 (7.5)
(7.5)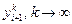 . Достаточное условие сходимости метода простой итерации выглядит следующим образом:
. Достаточное условие сходимости метода простой итерации выглядит следующим образом: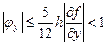
 . В качестве начального значения для итерационного процесса (7.5) можно использовать приближенное решение
. В качестве начального значения для итерационного процесса (7.5) можно использовать приближенное решение 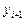 , полученное с помощью явной схемы Адамса:
, полученное с помощью явной схемы Адамса: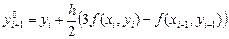
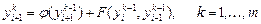
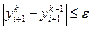
 (8.1)
(8.1) этого уравнения на отрезке [0,1]. Любой отрезок [ a,b ] можно привести к этому отрезку с помощью замены переменной
этого уравнения на отрезке [0,1]. Любой отрезок [ a,b ] можно привести к этому отрезку с помощью замены переменной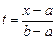
 (8.2)
(8.2) (8.3)
(8.3)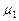 - точка на оси ординат, в которой помещается начало искомой интегральной кривой;
- точка на оси ординат, в которой помещается начало искомой интегральной кривой;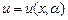 зависящим от параметра α, будем искать такое значение параметра
зависящим от параметра α, будем искать такое значение параметра 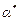 , при котором
, при котором  (т.е. при котором интегральная кривая попадет в точку с координатами (1, μ)). Тогда решение задачи Коши (8.1), (8.3) совпадет с решением краевой задачи (8.1), (8.2). Условие попадания интегральной кривой в точку (1, μ) модно сформулировать в виде нелинейного уравнения относительно неизвестного α:
(т.е. при котором интегральная кривая попадет в точку с координатами (1, μ)). Тогда решение задачи Коши (8.1), (8.3) совпадет с решением краевой задачи (8.1), (8.2). Условие попадания интегральной кривой в точку (1, μ) модно сформулировать в виде нелинейного уравнения относительно неизвестного α: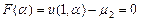 (8.4)
(8.4) , содержащий значение
, содержащий значение 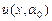 должно при x = 1 находится ниже точки μ 2, а
должно при x = 1 находится ниже точки μ 2, а  - выше. Далее полагая
- выше. Далее полагая
 и в соответствии с методом деления отрезка пополам отбрасываем один из отрезков
и в соответствии с методом деления отрезка пополам отбрасываем один из отрезков  или
или  , на котором функция F (α) не меняет знак и т.д. Процесс поиска решения прекращается, если разность двух последовательно найденных значений α меньше некоторого наперед заданного числа.
, на котором функция F (α) не меняет знак и т.д. Процесс поиска решения прекращается, если разность двух последовательно найденных значений α меньше некоторого наперед заданного числа.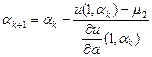 (8.5)
(8.5) , то формула (8.5) преобразуется в следующую
, то формула (8.5) преобразуется в следующую (8.6)
(8.6)