П.3.2. Устойчивость схемы Эйлера на модельной задаче
Для разностных схем, используемых в приближенном решении дифференциальных уравнений, естественно требовать выполнения свойства устойчивости
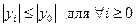 . .
Свойство устойчивости разностных схем связано с их сходимостью.
Исследуем устойчивость схемы Эйлера на примере решения модельного уравнения (3.3).
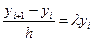 или или 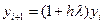 , ,
т.е. 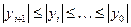 , если , если 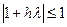 , т.е. для устойчивости достаточно выполнения условий , т.е. для устойчивости достаточно выполнения условий 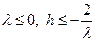 . .
Т.о., явная схема Эйлера условно устойчива, поскольку накладывается условие на шаг. Действительно, легко убедиться в том, что при большом шаге схема становиться неустойчивой при 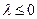 . .
Пусть, например, 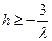 , тогда , тогда 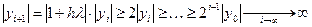 , т.е. схема неустойчива. , т.е. схема неустойчива.
Иначе обстоит дело с неявной схемой Эйлера. Рассмотрим ту же модельную задачу
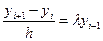 или или 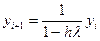
и схема устойчива при 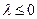 для для 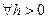 , поскольку , поскольку 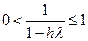 . .
Дата добавления: 2015-01-18 | Просмотры: 787 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
