П.6.2. Построение явной схемы Адамса
Для построения квадратурной формулы применим интерполяционную формулу Ньютона с разделенными разностями.
Пусть  . Заменим . Заменим 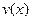 интерполяционным многочленом Ньютона, построенным по узлам интерполяционным многочленом Ньютона, построенным по узлам  : :
 , ,
где 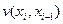 , ,  , … - разделенные разности. , … - разделенные разности.
Выполним замену переменной по формуле  и введем обозначения и введем обозначения
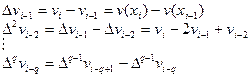
Учитывая, что  и и 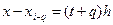 можно выписать соотношения для разделенных разностей можно выписать соотношения для разделенных разностей
 , и т.д. , и т.д.
Тогда интерполяционный многочлен можно записать в следующем виде:
 , ,
где  - остаточный член. - остаточный член.
Квадратурная формула примет вид
 , (6.7) , (6.7)
где  , , 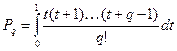
В частности  и т.д. и т.д.
Т.о., из формул (6.7) и (6.6) можно получить общий вид явной q -шаговой схемы Адамса:
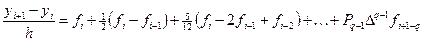 (6.8) (6.8)
В частности, двухшаговая схема принимает вид:
 (6.9) (6.9)
а трехшаговая
 (6.10) (6.10)
где  . .
Дата добавления: 2015-01-18 | Просмотры: 761 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
