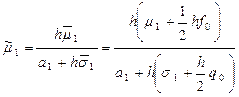|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Интегро-интерполяционный метод построения разностных схем (метод баланса)Обычно дифференциальное уравнение выражает некоторый физический закон сохранения. Этот закон можно записать в интегральной форме для интервала сетки (уравнение баланса). Дифференциальное уравнение получается из уравнения баланса при стремлении шага сетки к нулю в предположении существования непрерывных производных, входящих в уравнение. Входящие в уравнение баланса на сетке производные и интегралы следует заменить приближенными выражениями на сетке. Такой метод называется интегро-интерполяционным методом или методом баланса. Применим этот метод для построения разностной схемы следующей краевой задачи для ОДУ 2-го порядка:
где
Для построения разностной схемы введем на отрезке [0,1] равномерную сетку с шагом h:
Обозначим
Это уравнение представляет собой уравнение баланса тепла на отрезке Чтобы получить из (10.3) трехточечное разностное уравнение, заменим
Проинтегрируем равенства
В результате получаем из (10.3) схему
При выводе мы фактически предполагали лишь, что Напишем разностную аппроксимацию для краевого условия третьего рода
Для этого воспользуемся уравнением баланса при
Подставим сюда Заменим всюду u на y, получим разностное краевое условие
Перепишем его в следующем виде
где Оценим на решении u = u(x) уравнения (10.1) величину невязки
Подставим
получим
т.е. разностное краевое условие третьего рода (10.5) аппроксимирует условие Объединяя уравнения (10.4) и (10.5) получим следующую разностную схему для задачи (10.1)-(10.2):
Систему (10.6) можно записать в виде
где Ai = ai, Bi = ai+1, Ci = ai+1 + ai + h2di, Fi = h2jI,
Данная система решается методом прогонки. Дата добавления: 2015-01-18 | Просмотры: 2123 | Нарушение авторских прав |
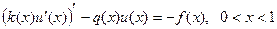 (10.1)
(10.1) (10.2)
(10.2)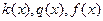 - заданные, достаточно гладкие функции, удовлетворяющие условиям
- заданные, достаточно гладкие функции, удовлетворяющие условиям .
.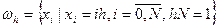
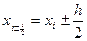 ,
, 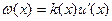 ,
, 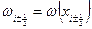 . Проинтегрируем уравнение (10.1) на отрезке
. Проинтегрируем уравнение (10.1) на отрезке 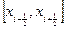 , тогда получим уравнение
, тогда получим уравнение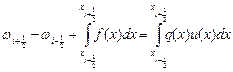 (10.3)
(10.3)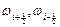 и интегралы в уравнении (10.3) линейной комбинацией значений подынтегральных функций в узлах сетки
и интегралы в уравнении (10.3) линейной комбинацией значений подынтегральных функций в узлах сетки 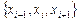 , например
, например ,
, 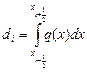
 по x от xi- 1 до xi
по x от xi- 1 до xi ,
,
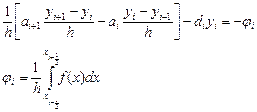 (10.4)
(10.4)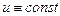 при
при 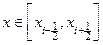 ,
, 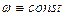 при
при  .
.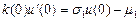
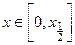 , где
, где 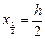
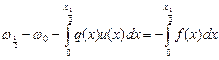
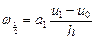 ,
, 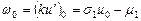 ,
,  ,
, 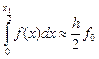 .
.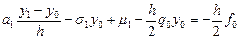
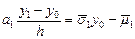 , (10.5)
, (10.5)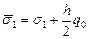 ,
, 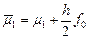
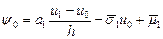 .
. ,
,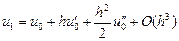 ,
,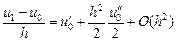
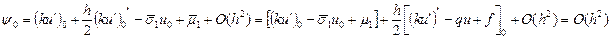 ,
,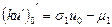 при x = 0 с погрешностью второго порядка
при x = 0 с погрешностью второго порядка  .
. , (10.6)
, (10.6)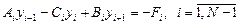 ,
, ,
,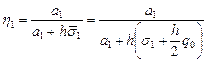 ,
,