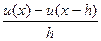|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.2.1. Разностная схема
Метод Эйлера – простейший одношаговый метод. Его можно выводить исходя из разных соображений. Например, пусть u(x) – скалярная непрерывная дифференцируемая функция, т.е. в каждой точке x существует производная
тогда при малых h
и выражение Рассмотрим задачу Коши для дифференциального уравнения первого порядка
На отрезке
Система (2.2.) называется разностной схемой Эйлера. Для нахождения
Аналогично можно получит неявную схему Эйлера
В этом случае, в качестве разностной аппроксимации для производной используется выражение Дата добавления: 2015-01-18 | Просмотры: 743 | Нарушение авторских прав |
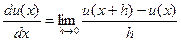
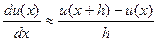
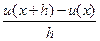 можно использовать для разностной аппроксимации первой производной.
можно использовать для разностной аппроксимации первой производной. (2.1)
(2.1)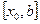 введем сетку с шагом h, и в узлах сетки заменим производную ее разностной аппроксимацией. В результате получим систему уравнений для нахождения сеточной функции
введем сетку с шагом h, и в узлах сетки заменим производную ее разностной аппроксимацией. В результате получим систему уравнений для нахождения сеточной функции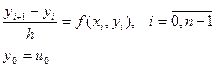 (2.2)
(2.2)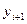 имеем явную формулу
имеем явную формулу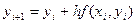 (2.3)
(2.3)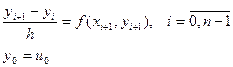 (2.4)
(2.4)