 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.3.1. Устойчивость задачи Коши по начальным данным
Рассмотрим задачу Коши
Пусть
где Решая дифференциальное уравнение, получаем
Следовательно, если наложить условие Решение задачи (3.2) при
Это уравнение можно рассматривать как модельное при исследовании устойчивости. Решение этого уравнения имеет вид Дата добавления: 2015-01-18 | Просмотры: 807 | Нарушение авторских прав |
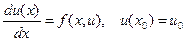 (3.1)
(3.1) - решение задачи коши с начальным условием
- решение задачи коши с начальным условием 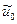 . Тогда для погрешности
. Тогда для погрешности  можно написать дифференциальное уравнение
можно написать дифференциальное уравнение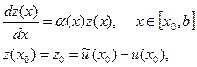 (3.2)
(3.2) .
.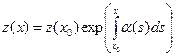 .
.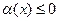 , т.е.
, т.е. 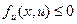 , то
, то 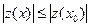 или
или 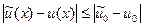 , т.е. решение задачи Коши устойчиво по начальным данным (погрешность не возрастает). Если же
, т.е. решение задачи Коши устойчиво по начальным данным (погрешность не возрастает). Если же 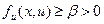 , то получаем неравенство
, то получаем неравенство 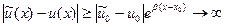 при
при 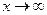 , т.е. решение задачи Коши неустойчиво по начальным данным.
, т.е. решение задачи Коши неустойчиво по начальным данным.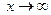 ведет себя аналогично решению линейного уравнения
ведет себя аналогично решению линейного уравнения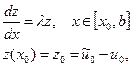 (3.3)
(3.3) . Его модуль не возрастает при
. Его модуль не возрастает при 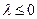 , т.е.
, т.е.  и решение устойчиво.
и решение устойчиво.