 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.4.2. Построение семейства схем второго порядка тосностиИдея построения семейства разностных схем 2-го порядка точности состоит в следующем: Пусть u(x) – решение задачи Коши
Разлагая решение по формуле Тейлора на интервале сетки
В простейшем случае, ограничиваясь только первым членом разложения и заменяя
Можно предположить, что для получения схемы второго порядка точности надо в разложении (4.2) сохранить член со второй производной. Заменим
при соответствующем выборе величин
Из формул (4.2)-(4.4) получаем
Эта формула дает нам право искать разностные схемы второго порядка точности в следующем виде:
где α, b, g - параметры, подлежащие определению. Рассмотрим погрешность аппроксимации для схемы (4.5):
где Тогда можно вывести следующие соотношения:
С учетом этих соотношений погрешность аппроксимации примет вид:
Следовательно, чтобы погрешность аппроксимации имела второй порядок малости относительно h, необходимо и достаточно выполнения условий
Их можно переписать в следующем виде
введем обозначение
где s - любое ненулевое число. Численные методы решения задачи Коши, использующие разностные схемы семейства (4.6), называются методами Рунге-Кутта второго порядка точности. Схему (4.6) можно переписать в форме «предикатор-корректор», в которой сначала считается промежуточное значение
В частности, при
При
Дата добавления: 2015-01-18 | Просмотры: 776 | Нарушение авторских прав |
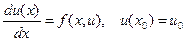
 длины h, имеем
длины h, имеем (4.2)
(4.2) на f(x,u), получаем для приближенного решения явную схему Эйлера, которая имеет 1-ый порядок точности
на f(x,u), получаем для приближенного решения явную схему Эйлера, которая имеет 1-ый порядок точности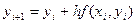 .
.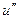 конечной разностью:
конечной разностью: (4.3)
(4.3)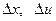 . Причем для
. Причем для  можно указать приближенную формулу
можно указать приближенную формулу (4.4)
(4.4)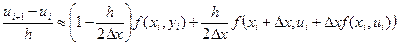
 , (4.5)
, (4.5)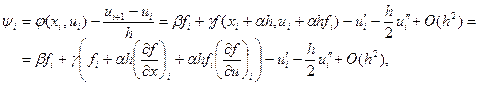
 ,
,  ,
, 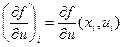 ,
, 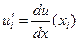 ,
,  .
.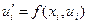 ,
, 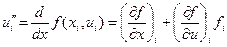

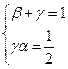
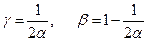
 , тогда семейство разностных схем (4.5), имеющих погрешность аппроксимации второго порядка, принимает вид однопараметрического семейства:
, тогда семейство разностных схем (4.5), имеющих погрешность аппроксимации второго порядка, принимает вид однопараметрического семейства: , (4.6)
, (4.6)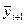 , а затем оно корректируется:
, а затем оно корректируется: (4.7)
(4.7) , получаем схему Эйлера-Коши:
, получаем схему Эйлера-Коши: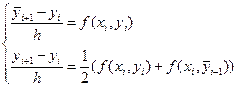 (4.8)
(4.8) - модифицируемую схему Эйлера:
- модифицируемую схему Эйлера: (4.9)
(4.9)