 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.7.2. Погрешность аппроксимации и устойчивость на модельной задачеПогрешность аппроксимации для схемы (7.2) определяется следующим образом:
где Справедливы следующие разложения
С учетом этих разложений формула (7.3) примет вид:
Однако, очевидно, что Следовательно, двухточечная неявная схема Адамса имеет третий порядок аппроксимации. Исследуем устойчивость схемы (7.2) на модельной задаче
Для этой задачи схема (7.2) примет форму трехточечного разностного уравнения с постоянными коэффициентами
Подставляя в это уравнение частное решение вида
или
где Поскольку a > 0 для любого l < 0, то дискриминант этого уравнения
Условие на корни
Это значит, что для устойчивости разностной схемы достаточно выполнения неравенства:
что равносильно ограничению на шаг разностной схемы
Дата добавления: 2015-01-18 | Просмотры: 682 | Нарушение авторских прав |
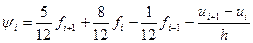 (7.3)
(7.3)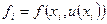 , u(x) – точное решение задачи Коши.
, u(x) – точное решение задачи Коши.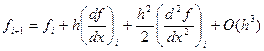 ,
,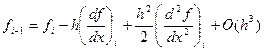 ,
,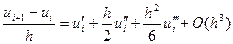 .
.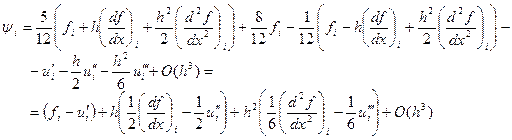
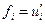 ,
, 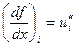 ,
, 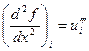 , поэтому для погрешности аппроксимации получаем
, поэтому для погрешности аппроксимации получаем 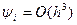
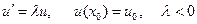
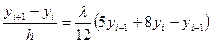
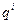 , получим квадратное уравнение для q:
, получим квадратное уравнение для q: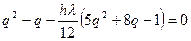
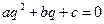 ,
,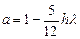 ,
, 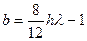 ,
, 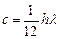 .
.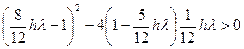 для любого l < 0.
для любого l < 0. выполняется, если
выполняется, если 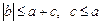 , т.к.
, т.к.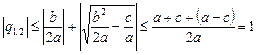
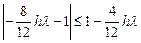 ,
,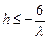 .
.