|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
П.2.3. Сходимость Метода Эйлера
Пусть zi – погрешность приближенного решения в узлах сетки, т.е.
 (2.9) (2.9)
Тогда 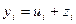 , кроме того , кроме того
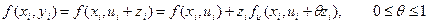 (2.10) (2.10)
Следовательно, можно получить соотношение
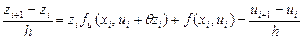 (2.11) (2.11)
или
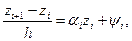 (2.12) (2.12)
где 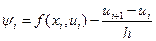 , ,  . .
В итоге получим
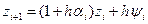 (2.13) (2.13)
или  (2.14) (2.14)
Т.о., если выполнено условие
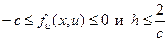 (2.15) (2.15)
то 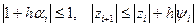
или
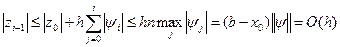 (2.16) (2.16)
Итак, можно сделать вывод, что при выполнении условия (2.15)
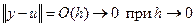 , ,
т.е. метод Эйлера сходиться к точному решению с первым порядком относительно h, т.е. имеет первый порядок точности.
В случае неявной схемы Эйлера для погрешности решения получим формулу
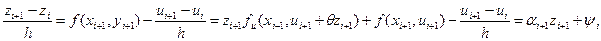 , ,
где 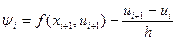 , ,

В итоге получаем 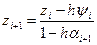 . .
Если поставить условие 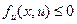 , то , то 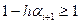 , ,
тогда 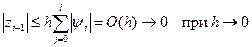
Дата добавления: 2015-01-18 | Просмотры: 828 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
