Сходимость методов Рунге-Кутта второго порядка
Рассмотрим вопрос о сходимости схем семейства (4.6) в применении к модельной задаче:

разностная схема (4.6) принимает вид:
 (5.1) (5.1)
Выражая  , получаем , получаем
 (5.2) (5.2)
введем теперь рекуррентную формулу для погрешности разностной схемы
 (5.3) (5.3)
Поскольку
 , ,
то рекуррентную формулу для погрешности можно записать в следующем виде
 , (5.4) , (5.4)
где  . .
Разложим функцию  и и  в ряд Тейлора в окрестности в ряд Тейлора в окрестности  , тогда , тогда
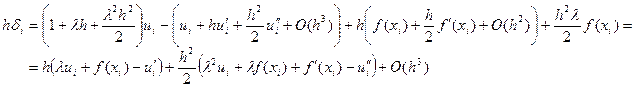
но
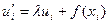 , ,

поэтому  или или  . .
Нетрудно убедиться, что q >0 для любых l, h и q ≤1 при условии 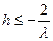 , т.е. , т.е. 
Тогда из формулы (5.4) следует
 , ,
т.е. схемы Рунге-Кутты второго порядка сходятся и имеют второй порядок точности для модельной задачи.
Дата добавления: 2015-01-18 | Просмотры: 704 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|
