 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.6.1. Сценарий построения разностных схемДля решения задачи коши
Рассмотренные ранее одношаговые методы являются частным случаем формы (6.1). Например, при q = 1, b0 = 0, b1 = a0 = 1, a1 = -1 получаем явную схему Эйлера. Схема (6.1) будет явной, если b0 = 0 (в таком случае она называется экстрополяционной). Значения yi+1 будут тогда определятся из предыдущих значений по явной формуле:
Вычисления начинаются с Если
Это уравнение можно решать, например методом Ньютона. Погрешность аппроксимации схемы (6.1) определяется формулой
где Если Коэффициенты в схеме (6.1) выбираются из условия устойчивости и аппроксимации. Кроме того, поскольку коэффициенты схемы определены с точностью до постоянного множителя, можно считать, что
Учитывая, что
Разлагая (6.4) по степеням h и требуя, чтобы погрешность имела заданный порядок, получим остальной набор параметров для нахождения Исторически первые многошаговые схемы появились способом, отличным от вышеизложенного. Если проинтегрировать дифференциальное уравнение на отрезке
Заменяя теперь в этом соотношении интеграл некоторой квадратурной формулой, выведенной с помощью замены подынтегральной функции интерполяционным многочленом, построенным по узлам
где Очевидно, что формула (6.6) частный случай разностной схемы (6.1). Дата добавления: 2015-01-18 | Просмотры: 982 | Нарушение авторских прав |
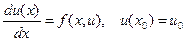 наиболее употребительными являются q-шаговые методы вида
наиболее употребительными являются q-шаговые методы вида (6.1)
(6.1) (6.2)
(6.2) . Чтобы найти
. Чтобы найти  , надо знать значения сеточной функции
, надо знать значения сеточной функции 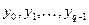 . Их приходится вычислять с помощью какого-нибудь другого метода, напр. Метода Рунге-Кутта, используя начальное значение
. Их приходится вычислять с помощью какого-нибудь другого метода, напр. Метода Рунге-Кутта, используя начальное значение  .
. , то схема (6.1) будет неявной (интерполяционной). Тогда для нахождения yi+1 необходимо решать нелинейное уравнение:
, то схема (6.1) будет неявной (интерполяционной). Тогда для нахождения yi+1 необходимо решать нелинейное уравнение: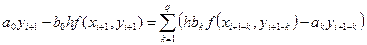 (6.3)
(6.3) , (6.4)
, (6.4) - точное решение задачи Коши.
- точное решение задачи Коши.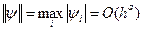 , то схема имеет порядок аппроксимации, равный a.
, то схема имеет порядок аппроксимации, равный a. .
. есть решение дифференциального уравнения при
есть решение дифференциального уравнения при  , можно получить второе условие из (6.1)
, можно получить второе условие из (6.1) .
. .
. , то получим формулу
, то получим формулу (6.5)
(6.5) , получим разностную схему
, получим разностную схему , (6.6)
, (6.6) - квадратурная формула.
- квадратурная формула.