 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.9.4. Краевые условия 2-го и 3-го родаРассмотрим уравнение (9.3) с краевыми условиями 2-го или 3-го рода
Будем решать эту задачу с помощью трехточечной разностной схемы (9.6) с условиями на коэффициенты (9.9). При этих условиях, как было показано, схема имеет второй порядок аппроксимации. В таком случае возникает вопрос: как аппроксимировать краевые условия? Если пользоваться для этого односторонними разностными производными, как в методе Эйлера, то краевые условия запишутся в виде
однако, такие формулы будут иметь погрешность аппроксимации первого порядка. Чтобы краевые условия не снижали порядок аппроксимации разностной схемы (9.6), необходимо воспользоваться односторонними разностными аппроксимациями производных, имеющими второй порядок по h. Например, для этих целей подходит разностная производная
где Действительно, по формулам Тейлора
поэтому
При использовании подобных формул разностные аппроксимации краевых условий принимают вид
В такой ситуации для разрешения трехточечной схемы (9.5) также может быть использован метод прогонки. Действительно, уравнение
на левом краю интервала составляет с краевым условием систему
из которой можно исключить
с некоторыми вполне определенными коэффициентами
где коэффициенты
из которой можно найти Дата добавления: 2015-01-18 | Просмотры: 764 | Нарушение авторских прав |
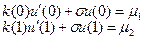
 ,
, ,
,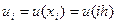
 ,
,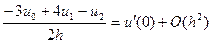
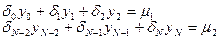
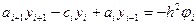
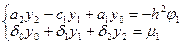
 , при этом система преобразуется в уравнение
, при этом система преобразуется в уравнение
 . Остальные
. Остальные  находятся по формулам
находятся по формулам (9.16)
(9.16) считаются по рекуррентным формулам (9.14), исходя из значений
считаются по рекуррентным формулам (9.14), исходя из значений  ,
, , а следом - и все остальные
, а следом - и все остальные