 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.2.2. Погрешность аппроксимации
Определение 2.1. Невязка, получающаяся при подстановке точного решения u(x) исходной задачи в разностную схему, называется погрешностью аппроксимации разностной схемы. Рассмотрим погрешность аппроксимации схемы (2.2)
где С учетом того, что
Если ввести норму погрешности аппроксимации То же верно и для неявной схемы Эйлера. Действительно для нее
поэтому
Дата добавления: 2015-01-18 | Просмотры: 703 | Нарушение авторских прав |
 (2.5)
(2.5)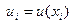
 можно получит для
можно получит для 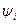 следующее выражение:
следующее выражение: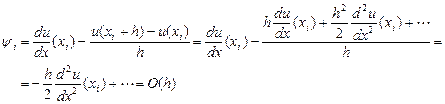 (2.6)
(2.6) , то она также будет иметь первый порядок малости относительно h, т.е.
, то она также будет иметь первый порядок малости относительно h, т.е.  . В связи с этим говорят, что явная схема Эйлера имеет первый порядок аппроксимации.
. В связи с этим говорят, что явная схема Эйлера имеет первый порядок аппроксимации. (2.7)
(2.7) (2.8)
(2.8)