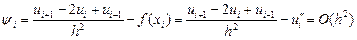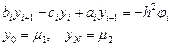|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.9.1. Простейшая задача. Разностная аппроксимация второй производной
Рассмотрим простейшую краевую задачу
Введем на отрезке [0,1] равномерную сетку
Попробуем аппроксимировать
Разложим
Тогда погрешность аппроксимации выразится следующим образом:
Потребуем, чтобы выполнялись условия
Тогда
Применяя эту аппроксимацию к задаче (9.1) получим разностную схему для этой задачи
Погрешность аппроксимации этой схемы имеет второй порядок
Разностная схема (9.2) сводится к решению системы линейных уравнений с трехдиагональной матрицей. Такие методы называются трехточечными. В общем виде такую схему можно записать в стандартной форме:
Эта форма записи называется прогоночным видом трехточечной разностной схемы.
Дата добавления: 2015-01-18 | Просмотры: 882 | Нарушение авторских прав |
 (9.1)
(9.1)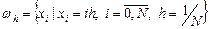
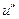 с помощью значений функции
с помощью значений функции  в узлах сетки. Для подбора аппроксимационной формулы воспользуемся методом неопределенных коэффициентов:
в узлах сетки. Для подбора аппроксимационной формулы воспользуемся методом неопределенных коэффициентов: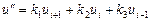 .
.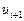 и
и  по степеням h
по степеням h
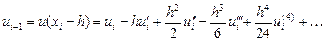
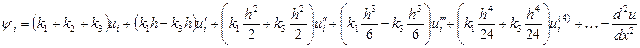
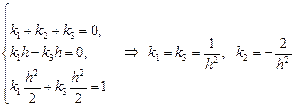
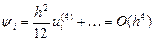 и аппроксимация второй производной имеет вид
и аппроксимация второй производной имеет вид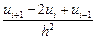
 (9.2)
(9.2)