 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Второй замечательный предел и его следствияТеорема 1 (2-й замечательный предел). Справедливо равенство Доказательство. Воспользуемся известным пределом сначала, что
Из неравенств
Таким образом,
Поскольку
и при Рассмотрим теперь
= Таким образом, и Обозначим Следствия. 1) 2) 3) Доказательство. 1) При 2) Положим
3) Заметим, что Из следствий имеем: при Примеры. 1) 2)
Дата добавления: 2015-01-18 | Просмотры: 1036 | Нарушение авторских прав |
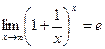 , где
, где  .
. . Докажем
. Докажем . Обозначим целую часть х через n:
. Обозначим целую часть х через n: 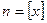 . Тогда
. Тогда  и, следовательно,
и, следовательно,  и
и  . Из неравенств
. Из неравенств и
и  следует, что
следует, что .
. и
и  следует, что
следует, что .
. , где
, где  ,
,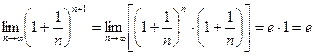
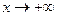 и
и 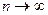 , по теореме о промежуточной переменной имеем, что
, по теореме о промежуточной переменной имеем, что 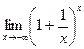 . Положим
. Положим  . Когда
. Когда 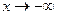 , то
, то  и
и =
=  =
=  =
=  =
= =
=  .
. . Значит, мы доказали, что
. Значит, мы доказали, что  . Если
. Если 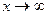 , то
, то  и 2-й замечательный предел примет вид
и 2-й замечательный предел примет вид  .
. . В частности,
. В частности,  .
. . В частности,
. В частности,  .
. .
. .
. получаем частный случай.
получаем частный случай. при
при  . Отсюда
. Отсюда 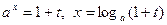 . Поэтому
. Поэтому . При
. При  , поэтому
, поэтому 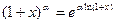 . Тогда
. Тогда 
 . Следствия доказаны.
. Следствия доказаны. ,
,  .
.
 .
.
 .
.