Точки разрыва функции, их классификация
Определение 1. Пусть функция  определена на промежутке Х и определена на промежутке Х и 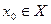 . Функция . Функция  называется непрерывной в точке называется непрерывной в точке  , если , если
 . (18.1) . (18.1)
Равенство (18.1) можно записать иначе:  , то есть для непрерывной функции знаки предела и функции можно поменять местами. , то есть для непрерывной функции знаки предела и функции можно поменять местами.
Очевидно, что о непрерывности функции можно говорить лишь по отношению к тем точкам  , в которых функция определена, то есть существует , в которых функция определена, то есть существует  . .
Пользуясь двумя определениями предела функции, можно дать определения непрерывности функции на языке последовательностей и на языке  . .
Определение 2. Функция  называется непрерывной в точке называется непрерывной в точке  , если для любой последовательности , если для любой последовательности 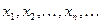 значений аргумента х, сходящейся к значений аргумента х, сходящейся к  , последовательность соответствующих значений функции , последовательность соответствующих значений функции 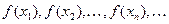 сходится к сходится к  . .
Определение 3. Функция  называется непрерывной в точке называется непрерывной в точке  , если для любого , если для любого 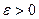 найдется найдется  , такое, что для всех х, удовлетворяющих неравенству , такое, что для всех х, удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство  . .
Определения 2 и 3 эквивалентны в силу теоремы 1 § 13.
Дадим еще одно определение непрерывности функции в точке – на языке приращений. Для этого положим  и назовем эту величину приращением аргумента х, а и назовем эту величину приращением аргумента х, а  – приращением функции в точке – приращением функции в точке  . .
Определение 4. Функция  называется непрерывной в точке называется непрерывной в точке  , если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть , если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть  . .
Последнее условие означает, что  , или , или  , или , или  , то есть определение 4 равносильно определению 1, а значит и определениям 2 и 3. , то есть определение 4 равносильно определению 1, а значит и определениям 2 и 3.
Определение 5. Функция  называется непрерывной в точке называется непрерывной в точке  справа (слева), если справа (слева), если  ( ( ). ).
Теорема 1. Функция  непрерывна в точке непрерывна в точке  тогда и только тогда, когда она непрерывна в этой точке одновременно и справа, и слева. тогда и только тогда, когда она непрерывна в этой точке одновременно и справа, и слева.
Доказательство. Поскольку  существует тогда и только тогда, когда существуют и равны односторонние пределы существует тогда и только тогда, когда существуют и равны односторонние пределы  и и  , причем , причем  = = = =  = =  , то , то  тогда и только тогда, когда тогда и только тогда, когда  = =  = =  . Теорема доказана. . Теорема доказана.
Определение 6. Функция  называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.
Если  , то при этом подразумевается непрерывность , то при этом подразумевается непрерывность  в точке в точке  справа, а в точке справа, а в точке  – слева. – слева.
Теорема 2. Если функции  и и  непрерывны в точке непрерывны в точке  , то функции , то функции 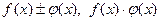 тоже непрерывны в точке тоже непрерывны в точке  . Если, кроме того, . Если, кроме того,  , то и функция , то и функция  непрерывна в точке непрерывна в точке  . .
Доказательство. Следует из теоремы 1 § 15 и определения 1 непрерывности функции в точке. Например,  , что и означает непрерывность функций , что и означает непрерывность функций  в точке в точке  . Остальные случаи рассматриваются аналогично. Теорема доказана. . Остальные случаи рассматриваются аналогично. Теорема доказана.
Теорема 3 (о непрерывности сложной функции). Пусть  и пусть существует окрестность точки и пусть существует окрестность точки  , в которой определена сложная функция. Если функция , в которой определена сложная функция. Если функция  непрерывна в точке непрерывна в точке  , а функция , а функция  непрерывна в точке непрерывна в точке  , то сложная функция , то сложная функция  непрерывна в точке непрерывна в точке  . .
Доказательство. В указанной в условии теоремы окрестности возьмем любую последовательность точек 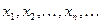 , сходящуюся к точке , сходящуюся к точке  , и пусть , и пусть 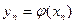 . Тогда, в силу непрерывности . Тогда, в силу непрерывности  в точке в точке  , ,  , то есть последовательность точек , то есть последовательность точек  сходится к точке сходится к точке 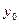 . Поэтому, в силу непрерывности . Поэтому, в силу непрерывности  в точке в точке 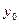 , ,  , то есть , то есть  . .
Теорема доказана.
Определение 7. Точка  называется точкой разрыва функции называется точкой разрыва функции  , если , если  определена в некоторой проколотой окрестности точки определена в некоторой проколотой окрестности точки  и не выполняется условие и не выполняется условие
 . .
В этом случае говорят также, что функция  является разрывной в точке является разрывной в точке  , или терпит разрыв в точке , или терпит разрыв в точке  , или имеет разрыв в точке , или имеет разрыв в точке  . .
Различают три типа точек разрыва.
1) Устранимый разрыв.
Определение 8. Точка  называется точкой устранимого разрыва функции называется точкой устранимого разрыва функции  , если существует конечный , если существует конечный  , но либо функция не определена в точке , но либо функция не определена в точке  , либо , либо  . .
Пример 1. Функция  имеет устранимый разрыв в точке имеет устранимый разрыв в точке  , ,
так как  . Этот разрыв можно устранить, изменив значение функции в точке . Этот разрыв можно устранить, изменив значение функции в точке  и положив и положив  . .
Вообще, если в точке  функция функция  имеет устранимый разрыв, то достаточно положить имеет устранимый разрыв, то достаточно положить  , чтобы функция стала непрерывной в точке , чтобы функция стала непрерывной в точке  . Иными словами, для восстановления непрерывности в точке . Иными словами, для восстановления непрерывности в точке  надо изменить значение надо изменить значение  в этой точке, если в этой точке, если  , или доопределить , или доопределить  в точке в точке  , если , если  . .
2) Разрыв 1-го рода.
Определение 9. Точка  называется точкой разрыва 1- го рода функции называется точкой разрыва 1- го рода функции  , если существуют конечные односторонние пределы , если существуют конечные односторонние пределы  и и  , но , но    . Разность . Разность   называют величиной скачка называют величиной скачка  в точке в точке  . .
Пример 2. Пусть  Тогда Тогда  = –1, = –1, 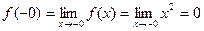 . .  и и  конечны, но не равны, поэтому точка конечны, но не равны, поэтому точка  – точка разрыва 1-го рода. Величина скачка равна – точка разрыва 1-го рода. Величина скачка равна  – –  = –1 – 0 = –1. = –1 – 0 = –1.
3) Разрыв 2-го рода.
Определение 10. Точка  называется точкой разрыва 2- го рода функции называется точкой разрыва 2- го рода функции  , если хотя бы один из односторонних пределов , если хотя бы один из односторонних пределов  и и  не существует или бесконечен. не существует или бесконечен.
Пример 3. Пусть  . Поскольку . Поскольку  , точка , точка  – точка разрыва 2-го рода. – точка разрыва 2-го рода.
Заметим, что  , то есть бесконечен один односторонний предел , то есть бесконечен один односторонний предел  . .
Пример 4. Пусть 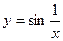 . Тогда . Тогда  не существует, поэтому не существует, поэтому  – точка разрыва 2-го рода. – точка разрыва 2-го рода.
При исследовании функций на непрерывность полезна
Теорема 4. Любая элементарная функция непрерывна в области своего определения.
Без доказательства.
Напомним, что элементарной функцией называется всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и композиций основных элементарных функций и постоянных, а основными элементарными функциями являются степенная  , показательная , показательная  , логарифмическая , логарифмическая  , тригонометрические , тригонометрические   , обратные тригонометрические функции , обратные тригонометрические функции   . .
Пример 5. Исследуем на непрерывность, непрерывность слева и справа, установим тип точек разрыва функции 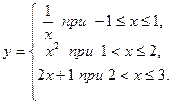
Решение. Заметим, что  . Поскольку функция не определена при . Поскольку функция не определена при 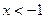 и при и при  , можно говорить только о непрерывности справа в точке , можно говорить только о непрерывности справа в точке  и о непрерывности слева в точке и о непрерывности слева в точке 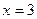 . Имеем . Имеем
 функция функция  непрерывна справа в точке непрерывна справа в точке  ; ;
 функция функция  непрерывна слева в точке непрерывна слева в точке 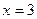 . .
Если  , то , то  – непрерывна как элементарная функция по теореме 4. Поскольку – непрерывна как элементарная функция по теореме 4. Поскольку  , то в точке , то в точке  функция функция  имеет разрыв 2 рода, причем она имеет разрыв 2 рода в этой точке и слева, и справа. имеет разрыв 2 рода, причем она имеет разрыв 2 рода в этой точке и слева, и справа.
Если  , то , то  – непрерывна как элементарная функция. – непрерывна как элементарная функция.
Если  , то , то  – непрерывна как элементарная функция. – непрерывна как элементарная функция.
Если 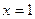 , то , то  , ,  , ,  , т. е. , т. е.
существует  , поэтому функция , поэтому функция  непрерывна в точке непрерывна в точке 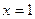 . .
Если  , то , то  , , 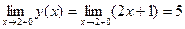 , , 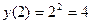 , т.е. в точке , т.е. в точке  односторонние пределы существуют, но не равны, поэтому в этой точке функция односторонние пределы существуют, но не равны, поэтому в этой точке функция  имеет разрыв 1 рода, величина скачка равна 1. Поскольку имеет разрыв 1 рода, величина скачка равна 1. Поскольку  , то функция , то функция  в точке в точке  непрерывна слева. непрерывна слева.
Таким образом, функция  непрерывна на множестве непрерывна на множестве  , непрерывна справа в точке , непрерывна справа в точке  , непрерывна слева в точках , непрерывна слева в точках  и и 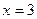 , имеет разрыв 2 рода в точке , имеет разрыв 2 рода в точке  и разрыв 1 рода в точке и разрыв 1 рода в точке  , величина скачка в этой точке равна 1. , величина скачка в этой точке равна 1.
Теорема 5 (о точках разрыва монотонной функции). Если функция  монотонна на интервале монотонна на интервале  , точка , точка 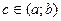 является точкой разрыва является точкой разрыва  , то с – точка разрыва 1-го рода. , то с – точка разрыва 1-го рода.
Доказательство. Пусть функция  не убывает на интервале не убывает на интервале  . Рассмотрим интервал . Рассмотрим интервал 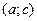 .Для всех значений х .Для всех значений х  имеем имеем  , т.е. , т.е.  ограничена сверху. В силу ограниченности сверху множества ограничена сверху. В силу ограниченности сверху множества  существует существует  . Покажем, что . Покажем, что 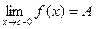 . Действительно, . Действительно,  для всех для всех  , так как А – верхняя граница значений , так как А – верхняя граница значений  . Возьмем . Возьмем 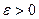 произвольно. Поскольку А – точная верхняя граница значений произвольно. Поскольку А – точная верхняя граница значений  , найдется , найдется  такое, что такое, что  . Тогда для . Тогда для  тем более тем более  в силу возрастания функции. Таким образом, для всех в силу возрастания функции. Таким образом, для всех 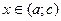  , для , для   и, значит, для и, значит, для   , т.е. , т.е. 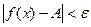 . Взяв . Взяв  , получим, что для всех х, таких, что , получим, что для всех х, таких, что  имеем имеем 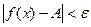 . А это и означает, что . А это и означает, что 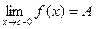 . .
Таким образом, доказано существование  . .
  Аналогично доказывается существование Аналогично доказывается существование 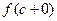 . .
В силу существования  и и 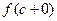 , с – точка разрыва 1 рода. , с – точка разрыва 1 рода.
Аналогично рассматривается случай невозрастающей функции.
Теорема доказана.
Таким образом, монотонная функция может иметь только точки разрыва 1-го рода.
Дата добавления: 2015-01-18 | Просмотры: 1036 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|

 не убывает на интервале
не убывает на интервале  . Рассмотрим интервал
. Рассмотрим интервал 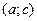 .Для всех значений х
.Для всех значений х  имеем
имеем  , т.е.
, т.е.  ограничена сверху. В силу ограниченности сверху множества
ограничена сверху. В силу ограниченности сверху множества  существует
существует  . Покажем, что
. Покажем, что 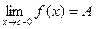 . Действительно,
. Действительно,  для всех
для всех  , так как А – верхняя граница значений
, так как А – верхняя граница значений  . Возьмем
. Возьмем 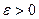 произвольно. Поскольку А – точная верхняя граница значений
произвольно. Поскольку А – точная верхняя граница значений  , найдется
, найдется  такое, что
такое, что  . Тогда для
. Тогда для  тем более
тем более  в силу возрастания функции. Таким образом, для всех
в силу возрастания функции. Таким образом, для всех 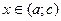
 , для
, для 
 и, значит, для
и, значит, для 
 , т.е.
, т.е. 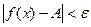 . Взяв
. Взяв  , получим, что для всех х, таких, что
, получим, что для всех х, таких, что  имеем
имеем 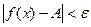 . А это и означает, что
. А это и означает, что 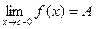 .
.
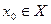 . Функция
. Функция  , если
, если . (18.1)
. (18.1) , то есть для непрерывной функции знаки предела и функции можно поменять местами.
, то есть для непрерывной функции знаки предела и функции можно поменять местами. .
. .
.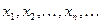 значений аргумента х, сходящейся к
значений аргумента х, сходящейся к 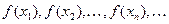 сходится к
сходится к  , такое, что для всех х, удовлетворяющих неравенству
, такое, что для всех х, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
. и назовем эту величину приращением аргумента х, а
и назовем эту величину приращением аргумента х, а  – приращением функции в точке
– приращением функции в точке  .
. , или
, или  , или
, или  (
( ).
). существует тогда и только тогда, когда существуют и равны односторонние пределы
существует тогда и только тогда, когда существуют и равны односторонние пределы  и
и  , причем
, причем  , то при этом подразумевается непрерывность
, то при этом подразумевается непрерывность  справа, а в точке
справа, а в точке  – слева.
– слева. непрерывны в точке
непрерывны в точке 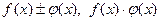 тоже непрерывны в точке
тоже непрерывны в точке  , то и функция
, то и функция  непрерывна в точке
непрерывна в точке  , что и означает непрерывность функций
, что и означает непрерывность функций  в точке
в точке  и пусть существует окрестность точки
и пусть существует окрестность точки  непрерывна в точке
непрерывна в точке  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция  непрерывна в точке
непрерывна в точке 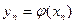 . Тогда, в силу непрерывности
. Тогда, в силу непрерывности  , то есть последовательность точек
, то есть последовательность точек  сходится к точке
сходится к точке 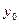 . Поэтому, в силу непрерывности
. Поэтому, в силу непрерывности  в точке
в точке  , то есть
, то есть  .
. .
. имеет устранимый разрыв в точке
имеет устранимый разрыв в точке  ,
, . Этот разрыв можно устранить, изменив значение функции в точке
. Этот разрыв можно устранить, изменив значение функции в точке  .
. , чтобы функция стала непрерывной в точке
, чтобы функция стала непрерывной в точке  , или доопределить
, или доопределить  .
.
 называют величиной скачка
называют величиной скачка  Тогда
Тогда  = –1,
= –1, 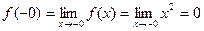 .
.  и
и  конечны, но не равны, поэтому точка
конечны, но не равны, поэтому точка  . Поскольку
. Поскольку  , точка
, точка  , то есть бесконечен один односторонний предел
, то есть бесконечен один односторонний предел 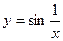 . Тогда
. Тогда  не существует, поэтому
не существует, поэтому  , показательная
, показательная  , логарифмическая
, логарифмическая  , тригонометрические
, тригонометрические 
 , обратные тригонометрические функции
, обратные тригонометрические функции 
 .
.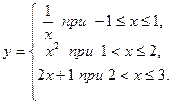
 . Поскольку функция не определена при
. Поскольку функция не определена при 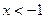 и при
и при  , можно говорить только о непрерывности справа в точке
, можно говорить только о непрерывности справа в точке  и о непрерывности слева в точке
и о непрерывности слева в точке 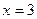 . Имеем
. Имеем функция
функция  непрерывна справа в точке
непрерывна справа в точке  функция
функция  , то
, то  – непрерывна как элементарная функция по теореме 4. Поскольку
– непрерывна как элементарная функция по теореме 4. Поскольку  , то в точке
, то в точке  , то
, то  – непрерывна как элементарная функция.
– непрерывна как элементарная функция. , то
, то  – непрерывна как элементарная функция.
– непрерывна как элементарная функция.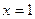 , то
, то  ,
,  ,
,  , т. е.
, т. е. , поэтому функция
, поэтому функция  , то
, то  ,
, 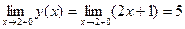 ,
, 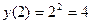 , т.е. в точке
, т.е. в точке  , то функция
, то функция  , непрерывна справа в точке
, непрерывна справа в точке 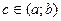 является точкой разрыва
является точкой разрыва  .
.
 Аналогично доказывается существование
Аналогично доказывается существование 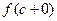 .
.