Критерий Коши существования предела
Определение 1. Пусть Е – бесконечное множество. Если любая окрестность 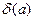 содержит точки множества Е, отличные от точки а, то а называется предельной точкой множества Е. содержит точки множества Е, отличные от точки а, то а называется предельной точкой множества Е.
Определение 2. (Генрих Гейне (1821-1881)). Пусть функция  определена на множестве Х и определена на множестве Х и  – предельная точка этого множества. Число А называется пределом функции – предельная точка этого множества. Число А называется пределом функции  в точке в точке  (или при (или при 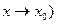 , если для любой последовательности значений аргумента , если для любой последовательности значений аргумента 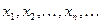 , сходящейся к , сходящейся к  и состоящей из чисел, отличных от и состоящей из чисел, отличных от  , соответствующая последовательность значений функции , соответствующая последовательность значений функции 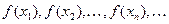 сходится к числу А. Пишут: сходится к числу А. Пишут: 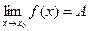 . .
Примеры. 1) Функция 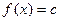 имеет предел, равный с, в любой точке числовой прямой. имеет предел, равный с, в любой точке числовой прямой.
Действительно, для любой точки  и любой последовательности значений аргумента и любой последовательности значений аргумента 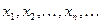 , сходящейся к , сходящейся к  и состоящей из чисел, отличных от и состоящей из чисел, отличных от  , соответствующая последовательность значений функции имеет вид , соответствующая последовательность значений функции имеет вид 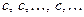 , а мы знаем, что эта последовательность сходится к с. Поэтому , а мы знаем, что эта последовательность сходится к с. Поэтому 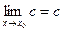 . .
2) Для функции 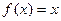 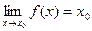 . .
Это очевидно, так как если  , то и , то и 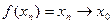 . .
3) Функция Дирихле 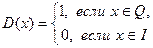 не имеет предела ни в одной точке. не имеет предела ни в одной точке.
Действительно, пусть 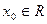 и и 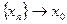 , причем все , причем все  – рациональные числа. Тогда – рациональные числа. Тогда  для всех n, поэтому для всех n, поэтому  . Если же . Если же 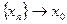 и все и все  – иррациональные числа, то – иррациональные числа, то 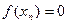 для всех n, поэтому для всех n, поэтому  . Мы видим, что условия определения 2 не выполняются, поэтому . Мы видим, что условия определения 2 не выполняются, поэтому 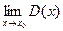 не существует. не существует.
4)  . .
Действительно, возьмем произвольную последовательность 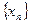 , сходящуюся к , сходящуюся к
числу 2. Тогда 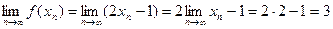 . Что и требовалось доказать. . Что и требовалось доказать.
Определение 3. (Коши (1789-1857)). Пусть функция  определена на множестве Х и определена на множестве Х и  – предельная точка этого множества. Число А называется пределом функции – предельная точка этого множества. Число А называется пределом функции  в точке в точке  (или при (или при 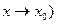 , если для любого , если для любого 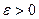 найдется найдется  , такое, что для всех значений аргумента х, удовлетворяющих неравенству , такое, что для всех значений аргумента х, удовлетворяющих неравенству
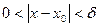 , ,
справедливо неравенство
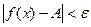 . .
Пишут: 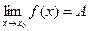 . .
Определение Коши можно дать и с помощью окрестностей, если заметить, что 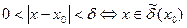 , а , а  : :
пусть функция  определена на множестве Х и определена на множестве Х и  – предельная точка этого множества. Число А называется пределомфункции – предельная точка этого множества. Число А называется пределомфункции  в точке в точке  , если для любой , если для любой 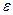 -окрестности точки А -окрестности точки А 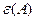 найдется проколотая найдется проколотая 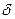 - окрестность точки - окрестность точки   ,такая, что ,такая, что 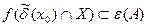 . .
Это определение полезно проиллюстрировать рисунком.
Пример 5. 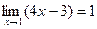 . .
Действительно, возьмем 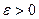 произвольно и найдем произвольно и найдем  , такое, что для всех х, удовлетворяющих неравенству , такое, что для всех х, удовлетворяющих неравенству 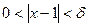 выполняется неравенство выполняется неравенство 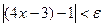 . Последнее неравенство равносильно неравенству . Последнее неравенство равносильно неравенству  , поэтому видим, что достаточно взять , поэтому видим, что достаточно взять 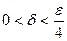 . Утверждение доказано. . Утверждение доказано.
Справедлива
Теорема 1. Определения предела функции по Гейне и по Коши эквивалентны.
Доказательство. 1) Пусть  по Коши. Докажем, что это же число является пределом и по Гейне. по Коши. Докажем, что это же число является пределом и по Гейне.
Возьмем 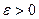 произвольно. Согласно определению 3 существует произвольно. Согласно определению 3 существует  , такое, что для всех , такое, что для всех  выполняется неравенство выполняется неравенство 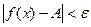 . Пусть . Пусть  – произвольная последовательность такая, что – произвольная последовательность такая, что  при при 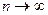 . Тогда существует номер N такой, что для всех . Тогда существует номер N такой, что для всех  выполняется неравенство выполняется неравенство 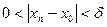 , поэтому , поэтому 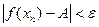 для всех для всех  , т.е. , т.е. 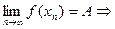 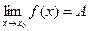 по Гейне. по Гейне.
2) Пусть теперь  по Гейне. Докажем, что по Гейне. Докажем, что  и по Коши. и по Коши.
Предположим противное, т.е. что 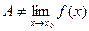 по Коши. Тогда существует по Коши. Тогда существует  такое, что для любого такое, что для любого  найдется найдется 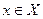 , , 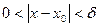 и и 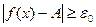 . Рассмотрим последовательность . Рассмотрим последовательность 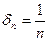 . Для указанного . Для указанного  и любого n существует и любого n существует 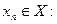 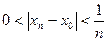 и и  . Это означает, что . Это означает, что 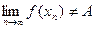 , хотя , хотя  , т.е. число А не является пределом , т.е. число А не является пределом  в точке в точке  по Гейне. Получили противоречие, которое и доказывает утверждение. Теорема доказана. по Гейне. Получили противоречие, которое и доказывает утверждение. Теорема доказана.
Теорема 2 (о единственности предела). Если существует предел функции в точке  , то он единственный. , то он единственный.
Доказательство. Если предел определен по Гейне, то его единственность вытекает из единственности предела последовательности. Если предел определен по Коши, то его единственность вытекает из эквивалентности определений предела по Коши и по Гейне. Теорема доказана.
Аналогично критерию Коши для последовательностей имеет место критерий Коши существования предела функции. Прежде чем его сформулировать, дадим
Определение 4. Говорят, что функция  удовлетворяет условию Коши в точке удовлетворяет условию Коши в точке  , если для любого , если для любого 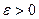 существует существует  , такое, что для любых значений , такое, что для любых значений 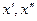 , таких, что , таких, что  и и 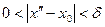 , выполняется неравенство , выполняется неравенство 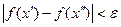 . .
Теорема 3 (критерий Коши существования предела). Для того чтобы функция  имела в точке имела в точке  конечный предел, необходимо и достаточно, чтобы в этой точке функция удовлетворяла условию Коши. конечный предел, необходимо и достаточно, чтобы в этой точке функция удовлетворяла условию Коши.
Доказательство. Необходимость. Пусть 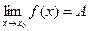 . Надо доказать, что . Надо доказать, что  удовлетворяет в точке удовлетворяет в точке  условию Коши. условию Коши.
Возьмем 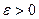 произвольно и положим произвольно и положим  . По определению предела для . По определению предела для 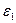 существует существует  , такое, что для любых значений , такое, что для любых значений 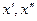 , удовлетворяющих неравенствам , удовлетворяющих неравенствам  и и 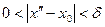 , выполняются неравенства , выполняются неравенства  и и 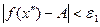 . Тогда . Тогда
 . Необходимость доказана. . Необходимость доказана.
Достаточность. Пусть функция  удовлетворяет в точке удовлетворяет в точке  условию Коши. Надо доказать, что она имеет в точке условию Коши. Надо доказать, что она имеет в точке  конечный предел. конечный предел.
Возьмем 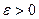 произвольно. По определению 4 найдется произвольно. По определению 4 найдется  , такое, что из неравенств , такое, что из неравенств  , , 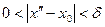 следует, что следует, что 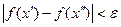 – это дано. – это дано.
Покажем сначала, что для всякой последовательности 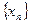 , сходящейся к , сходящейся к  , последовательность , последовательность  значений функции сходится. Действительно, если значений функции сходится. Действительно, если 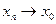 , то, в силу определения предела последовательности, для заданного , то, в силу определения предела последовательности, для заданного  найдется номер N, такой, что для любых найдется номер N, такой, что для любых 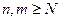 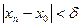 и и 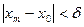 . Поскольку . Поскольку  в точке в точке  удовлетворяет условию Коши, имеем удовлетворяет условию Коши, имеем 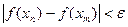 . Тогда по критерию Коши для последовательностей последовательность . Тогда по критерию Коши для последовательностей последовательность  сходится. Покажем, что все такие последовательности сходится. Покажем, что все такие последовательности  сходятся к одному и тому же пределу. Предположим противное, т.е. что есть последовательности сходятся к одному и тому же пределу. Предположим противное, т.е. что есть последовательности 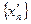 и и  , , 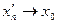 , , 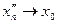 , такие, что , такие, что 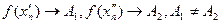 . Рассмотрим последовательность . Рассмотрим последовательность 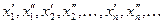 . Ясно, что она сходится к . Ясно, что она сходится к  , поэтому по доказанному выше последовательность , поэтому по доказанному выше последовательность  сходится, что невозможно, так как подпоследовательности сходится, что невозможно, так как подпоследовательности  и и 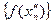 имеют разные пределы имеют разные пределы 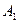 и и 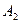 . Полученное противоречие показывает, что . Полученное противоречие показывает, что 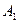 = = 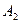 . Поэтому по определению Гейне функция имеет в точке . Поэтому по определению Гейне функция имеет в точке  конечный предел. Достаточность, а значит и теорема, доказаны. конечный предел. Достаточность, а значит и теорема, доказаны.
Дата добавления: 2015-01-18 | Просмотры: 1247 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|

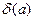 содержит точки множества Е, отличные от точки а, то а называется предельной точкой множества Е.
содержит точки множества Е, отличные от точки а, то а называется предельной точкой множества Е. определена на множестве Х и
определена на множестве Х и  – предельная точка этого множества. Число А называется пределом функции
– предельная точка этого множества. Число А называется пределом функции 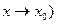 , если для любой последовательности значений аргумента
, если для любой последовательности значений аргумента 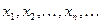 , сходящейся к
, сходящейся к 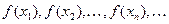 сходится к числу А. Пишут:
сходится к числу А. Пишут: 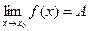 .
.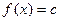 имеет предел, равный с, в любой точке числовой прямой.
имеет предел, равный с, в любой точке числовой прямой.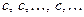 , а мы знаем, что эта последовательность сходится к с. Поэтому
, а мы знаем, что эта последовательность сходится к с. Поэтому 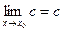 .
.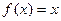
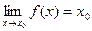 .
. , то и
, то и 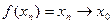 .
.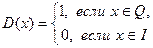 не имеет предела ни в одной точке.
не имеет предела ни в одной точке.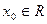 и
и 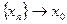 , причем все
, причем все  – рациональные числа. Тогда
– рациональные числа. Тогда  для всех n, поэтому
для всех n, поэтому  . Если же
. Если же 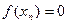 для всех n, поэтому
для всех n, поэтому  . Мы видим, что условия определения 2 не выполняются, поэтому
. Мы видим, что условия определения 2 не выполняются, поэтому 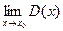 не существует.
не существует. .
.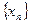 , сходящуюся к
, сходящуюся к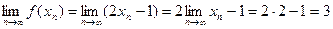 . Что и требовалось доказать.
. Что и требовалось доказать.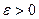 найдется
найдется  , такое, что для всех значений аргумента х, удовлетворяющих неравенству
, такое, что для всех значений аргумента х, удовлетворяющих неравенству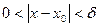 ,
,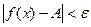 .
.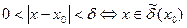 , а
, а  :
: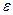 -окрестности точки А
-окрестности точки А 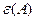 найдется проколотая
найдется проколотая 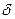 - окрестность точки
- окрестность точки  ,такая, что
,такая, что 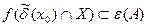 .
.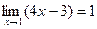 .
.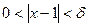 выполняется неравенство
выполняется неравенство 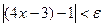 . Последнее неравенство равносильно неравенству
. Последнее неравенство равносильно неравенству  , поэтому видим, что достаточно взять
, поэтому видим, что достаточно взять 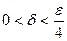 . Утверждение доказано.
. Утверждение доказано. по Коши. Докажем, что это же число является пределом и по Гейне.
по Коши. Докажем, что это же число является пределом и по Гейне. выполняется неравенство
выполняется неравенство  – произвольная последовательность такая, что
– произвольная последовательность такая, что 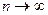 . Тогда существует номер N такой, что для всех
. Тогда существует номер N такой, что для всех  выполняется неравенство
выполняется неравенство 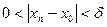 , поэтому
, поэтому 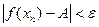 для всех
для всех 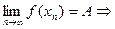
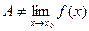 по Коши. Тогда существует
по Коши. Тогда существует  такое, что для любого
такое, что для любого 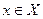 ,
, 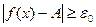 . Рассмотрим последовательность
. Рассмотрим последовательность 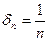 . Для указанного
. Для указанного 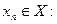
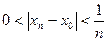 и
и  . Это означает, что
. Это означает, что 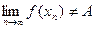 , хотя
, хотя 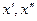 , таких, что
, таких, что  и
и 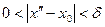 , выполняется неравенство
, выполняется неравенство 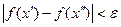 .
. . По определению предела для
. По определению предела для 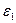 существует
существует  и
и 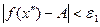 . Тогда
. Тогда . Необходимость доказана.
. Необходимость доказана. значений функции сходится. Действительно, если
значений функции сходится. Действительно, если 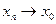 , то, в силу определения предела последовательности, для заданного
, то, в силу определения предела последовательности, для заданного 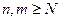
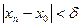 и
и 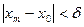 . Поскольку
. Поскольку 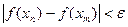 . Тогда по критерию Коши для последовательностей последовательность
. Тогда по критерию Коши для последовательностей последовательность 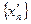 и
и  ,
, 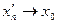 ,
, 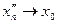 , такие, что
, такие, что 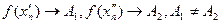 . Рассмотрим последовательность
. Рассмотрим последовательность 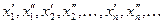 . Ясно, что она сходится к
. Ясно, что она сходится к  сходится, что невозможно, так как подпоследовательности
сходится, что невозможно, так как подпоследовательности  и
и 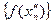 имеют разные пределы
имеют разные пределы 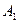 и
и 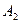 . Полученное противоречие показывает, что
. Полученное противоречие показывает, что