Равномерная непрерывность функций
В определении непрерывности функции  в точке в точке  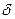 зависит, вообще говоря, не только от зависит, вообще говоря, не только от 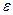 , но и от точки, т.е. , но и от точки, т.е.  Такая ситуация имеет место в случае произвольной функции Такая ситуация имеет место в случае произвольной функции  , т.е. в общем случае. Если же наложить на функцию , т.е. в общем случае. Если же наложить на функцию  некоторые условия, о которых речь пойдет дальше, то некоторые условия, о которых речь пойдет дальше, то  и от точки и от точки  не зависит. В этом случае мы получаем равномерно непрерывную на промежутке функцию. не зависит. В этом случае мы получаем равномерно непрерывную на промежутке функцию.
Определение 1. Функция  , заданная на некотором промежутке Х, называется равномерно непрерывной на этом промежутке, если для любого , заданная на некотором промежутке Х, называется равномерно непрерывной на этом промежутке, если для любого 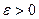 найдется такое найдется такое  , что неравенство , что неравенство 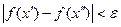 выполняется для любой пары точек выполняется для любой пары точек 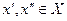 , удовлетворяющих неравенству , удовлетворяющих неравенству  . .
Теорема Кантора. Если функция  непрерывна на отрезке непрерывна на отрезке  , то она и равномерно непрерывна на этом отрезке. , то она и равномерно непрерывна на этом отрезке.
Георг Кантор (1845-1918) – немецкий математик, основатель современной теории множеств.
Доказательство. Предположим противное, т.е. что  непрерывна на отрезке непрерывна на отрезке  , ,
но не является на нем равномерно непрерывной. Это значит, что существует  такое, что при любом такое, что при любом  можно подобрать пару точек можно подобрать пару точек  , таких, что , таких, что  и и  . .
Возьмем последовательность значений 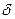 , сходящуюся к нулю: , сходящуюся к нулю: 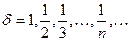 . .
Для 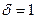 найдутся такие точки найдутся такие точки  , что , что  , но , но  . .
Для 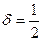 найдутся такие точки найдутся такие точки  , что , что  , но , но  . .
… … … … … … … … … … … … … … … … … … … …
Для  найдутся такие точки найдутся такие точки 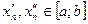 , что , что 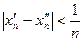 , но , но  . .
… … … … … … … … … … … … … … … … … … … …
В результате из отрезка  выделятся две ограниченные последовательности выделятся две ограниченные последовательности
 , (20.1) , (20.1)
 . (20.2) . (20.2)
Из последовательности (20.1) по теореме Больцано-Вейерштрасса можно выделить сходящуюся подпоследовательность. Чтобы не вводить новых обозначений, будем считать, что уже сама последовательность (20.1) сходится к некоторой точке  . Покажем, что тогда последовательность (20.2) тоже сходится к . Покажем, что тогда последовательность (20.2) тоже сходится к  . Действительно, поскольку . Действительно, поскольку 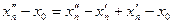 ,имеем ,имеем  при при 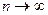 . .
По условию  непрерывна в точке непрерывна в точке  . Следовательно, . Следовательно, 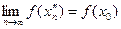 , поэтому , поэтому  , а это противоречит тому, что , а это противоречит тому, что  >0 для всех значений n. Полученное противоречие доказывает теорему. >0 для всех значений n. Полученное противоречие доказывает теорему.
Установим теперь факт, который будет нам нужен в интегральном исчислении.
Определение 2. Если функция  определена и ограничена на отрезке определена и ограничена на отрезке  , то разность между ее точными границами на этом отрезке называется колебанием функции на , то разность между ее точными границами на этом отрезке называется колебанием функции на  , т.е. колебание , т.е. колебание 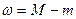 , где , где  , ,  . .
Следствие из теоремы Кантора. Если функция  определена и непрерывна на отрезке определена и непрерывна на отрезке  , то по заданному , то по заданному 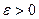 можно разбить этот отрезок на конечное число частей так, что на каждой из частей колебание функции не будет превышать можно разбить этот отрезок на конечное число частей так, что на каждой из частей колебание функции не будет превышать 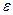 . .
Доказательство. По теореме Кантора функция  равномерно непрерывна на равномерно непрерывна на  . Поэтому по заданному . Поэтому по заданному 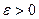 найдется найдется  такое, что для любых точек такое, что для любых точек  , удовлетворяющих неравенству , удовлетворяющих неравенству  , выполняется неравенство , выполняется неравенство 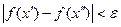 . Если отрезок . Если отрезок  разбить на такие части, чтобы длина каждой из них была меньше разбить на такие части, чтобы длина каждой из них была меньше 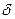 , то на каждой из отдельно взятых частей разность значений функции в любых двух точках по абсолютной величине будет меньше , то на каждой из отдельно взятых частей разность значений функции в любых двух точках по абсолютной величине будет меньше 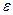 . В частности, это справедливо и для разности между наибольшим и наименьшим значениями функции на каждой из частей, которая и составляет колебание непрерывной функции на этой части. Следствие доказано. . В частности, это справедливо и для разности между наибольшим и наименьшим значениями функции на каждой из частей, которая и составляет колебание непрерывной функции на этой части. Следствие доказано.
Дата добавления: 2015-01-18 | Просмотры: 927 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|

 в точке
в точке 
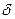 зависит, вообще говоря, не только от
зависит, вообще говоря, не только от 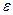 , но и от точки, т.е.
, но и от точки, т.е.  Такая ситуация имеет место в случае произвольной функции
Такая ситуация имеет место в случае произвольной функции  и от точки
и от точки 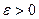 найдется такое
найдется такое  , что неравенство
, что неравенство 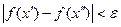 выполняется для любой пары точек
выполняется для любой пары точек 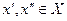 , удовлетворяющих неравенству
, удовлетворяющих неравенству  .
. , то она и равномерно непрерывна на этом отрезке.
, то она и равномерно непрерывна на этом отрезке. такое, что при любом
такое, что при любом  , таких, что
, таких, что  .
.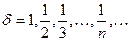 .
.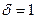 найдутся такие точки
найдутся такие точки  , что
, что  , но
, но  .
.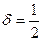 найдутся такие точки
найдутся такие точки  , что
, что  , но
, но  .
. найдутся такие точки
найдутся такие точки 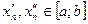 , что
, что 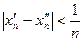 , но
, но  .
. , (20.1)
, (20.1) . (20.2)
. (20.2)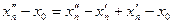 ,имеем
,имеем  при
при 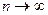 .
.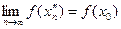 , поэтому
, поэтому  , а это противоречит тому, что
, а это противоречит тому, что 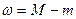 , где
, где  ,
,  .
.