 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Первый замечательный предел
Определение 1. Функция Например, Теорема 1. Для того чтобы Доказательство. Необходимость. Пусть Тогда Достаточность. Пусть Остановимся на сравнении бесконечно малых функций. Определение 2. Говорят, что функции Пишут: Определение 3. Говорят, что функции Покажем, что Теорема 2 (первый замечательный предел). Справедливо равенство
 Доказательство. Построим единичный круг и центральный угол Доказательство. Построим единичный круг и центральный угол  . .

    . (16.4) . (16.4)
Из (16.1)–(16.4) получаем
Разделив последнее неравенство на
Разделив
Поскольку Теореме о промежуточной переменной
Учитывая, что неравенство (16.6) сохраняется и для Установим теперь следствия первого замечательного предела. Покажем, что при
При раскрытии неопределенностей типа Теорема 3. Если
Доказательство. Имеем
Например, Замечание. В тех случаях, когда в числителе или знаменателе записана сумма, при раскрытии неопределенностей нельзя заменять отдельные слагаемые эквивалентными функциями, так как такая замена может привести к неверному результату. Например, в пределе
Рассмотрим теперь бесконечно большие функции. Определение 4. Если для любой последовательности значений аргумента Можно дать равносильное Определение Аналогично определяются соотношения Сравнивают бесконечно большие функции так же, как и бесконечно малые функции. Определение 5. Если Например, для функций
Дата добавления: 2015-01-18 | Просмотры: 805 | Нарушение авторских прав |
 называется бесконечно малой в окрестности точки
называется бесконечно малой в окрестности точки 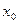 , если
, если  .
. – бесконечно малая функция в окрестности точки
– бесконечно малая функция в окрестности точки  , так как
, так как  .
. , необходимо и достаточно, чтобы имело место представление
, необходимо и достаточно, чтобы имело место представление  , где
, где 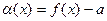 .
.
 . Теорема доказана.
. Теорема доказана. являются эквивалентными бесконечно малыми в окрестности точки
являются эквивалентными бесконечно малыми в окрестности точки  .
. .
. . Если же
. Если же  , то говорят, что
, то говорят, что  при
при  .
. .
. . (16.1)
Имеем
. (16.1)
Имеем
 , (16.2)
, (16.2)
 , (16.3)
, (16.3)


 .
. , получим
, получим . (16.5)
. (16.5) на каждую из частей этого неравенства, имеем
на каждую из частей этого неравенства, имеем . (16.6)
. (16.6) (см. (16.5))
(см. (16.5))  и
и  , по
, по , то есть
, то есть  . А так как
. А так как – функция четная, то
– функция четная, то  . Поэтому
. Поэтому . (16.7)
. (16.7) в силу четности всех входящих в него функций, из (16.7) и теоремы о промежуточной переменной получаем
в силу четности всех входящих в него функций, из (16.7) и теоремы о промежуточной переменной получаем 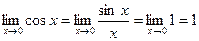 . Теорема доказана.
. Теорема доказана.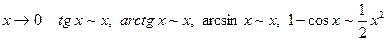 . Имеем
. Имеем при
при  при
при  при
при  при
при  полезна
полезна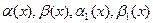 – бесконечно малые функции в окрестности точки
– бесконечно малые функции в окрестности точки  , то
, то .
.
 . Теорема доказана.
. Теорема доказана.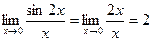 .
. нельзя заменить
нельзя заменить  на
на  и
и  , не имеющее смысла. Правильно вычислять предел так:
, не имеющее смысла. Правильно вычислять предел так: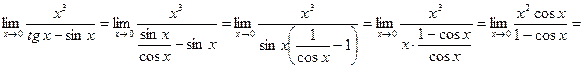
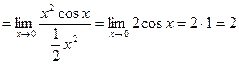 .
.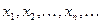 , сходящейся к
, сходящейся к  , то говорят, что функция
, то говорят, что функция  имеет в точке
имеет в точке  .
.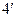 . Говорят, что функция
. Говорят, что функция  найдется такое число
найдется такое число  , что для всех значений
, что для всех значений 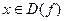
 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 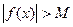 . В этом случае
. В этом случае 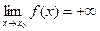 ,
, 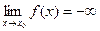 .
. и
и 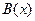 – бесконечно большие функции при
– бесконечно большие функции при  , то говорят, что
, то говорят, что  .
. и
и  , бесконечно больших при
, бесконечно больших при  , имеем
, имеем 
 , поэтому функции
, поэтому функции