 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Односторонние пределы
Определение 1 (Гейне). Число А называется правым пределом функции Определение 2 (Коши). Число А называется правым пределом функции
выполняется неравенство
Пишут: Совершенно аналогично даются определения односторонних пределов слева. Пишут: Пример 1. Пусть Имеет место Теорема 1. Для того чтобы функция
Это достаточно очевидно. Введем теперь понятие предела функции на бесконечности. Определение 3 (Гейне). Число А называется пределомфункции Определение 4 (Коши). Число А называется пределомфункции Пишут: Докажем, например, что Аналогично теореме 1 § 13 можно доказать эквивалентность определений 3 и 4. Справедлив также критерий Коши существования предела функции, когда Подобным же образом определяются пределы функции при
Дата добавления: 2015-01-18 | Просмотры: 743 | Нарушение авторских прав |
 в точке
в точке  (или пределом функции
(или пределом функции 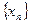 , сходящейся к
, сходящейся к  , соответствующая последовательность значений функции
, соответствующая последовательность значений функции  сходится к числу А.
сходится к числу А.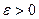 найдется
найдется  , такое, что для всех значений аргумента х, удовлетворяющих неравенству
, такое, что для всех значений аргумента х, удовлетворяющих неравенству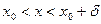 ,
,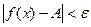 .
.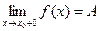 , а если
, а если  , то
, то  , или, короче,
, или, короче,  и
и 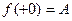 .
.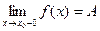 или
или  .
. Тогда
Тогда 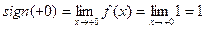 ,
, 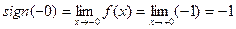 , поэтому
, поэтому  не существует.
не существует.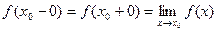 .
.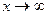 , если для любой бесконечно большой последовательности
, если для любой бесконечно большой последовательности 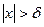 , выполняется неравенство
, выполняется неравенство 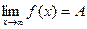 .
.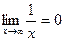 . Пусть
. Пусть 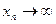 – произвольная бесконечно большая последовательность. Тогда, как известно,
– произвольная бесконечно большая последовательность. Тогда, как известно, 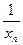 – бесконечно малая последовательность, поэтому
– бесконечно малая последовательность, поэтому 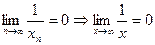 по определению 3.
по определению 3.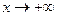 и
и 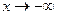 по Коши и по Гейне.
по Коши и по Гейне.