 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Арифметические операции над функциями, имеющими предел
Теорема 1. Пусть функции
Доказательство. Пусть
произвольно, то, в силу определения предела по Гейне, теорема доказана. Аналогичные теоремы имеют место в случае, когда Пример 1. С помощью теоремы 1 вычисляются следующие пределы:
Заметим, что для действительных функций имеют место теорема о промежуточной переменной и переход к пределу в неравенствах. Доказываются они с помощью соответствующих утверждений для последовательностей и определений предела по Гейне.
Дата добавления: 2015-01-18 | Просмотры: 1121 | Нарушение авторских прав |
 и
и  заданы на одном и том же множестве Х и имеют в точке
заданы на одном и том же множестве Х и имеют в точке  пределы, равные соответственно а и b. Тогда
пределы, равные соответственно а и b. Тогда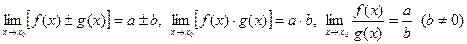 .
.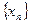 – произвольная сходящаяся к
– произвольная сходящаяся к 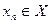 . Тогда, в силу определения предела функции в точке
. Тогда, в силу определения предела функции в точке 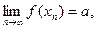
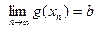 и по свойствам сходящихся последовательностей
и по свойствам сходящихся последовательностей 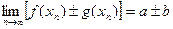 ,
, . Так как последовательность
. Так как последовательность 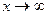 ,
, 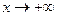 ,
, 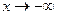 и для односторонних пределов.
и для односторонних пределов. – доказывается методом математической индукции,
– доказывается методом математической индукции,  ,
,  при условии, что
при условии, что 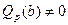 ,
, 
 .
.