 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П.9.3. Сходимость трехточечной разностной схемыДля исследования сходимости рассмотрим погрешность разностной схемы в узлах сетки:
Пользуясь линейностью оператора (9.7) и введенными ранее безиндексными обозначениями нетрудно установить, что погрешность в узлах сетки удовлетворяет разностной схеме
где y - погрешность аппроксимации. Введем оценку для погрешности в узлах сетки zi. Из соотношения (9.10) следует, что
поэтому схема (9.11) в прогоночном виде запишется следующим образом:
где Предположим, что в исходном линейном дифференциальном уравнении (9.3)
Тогда, в частности, имеет место неравенство
Значения zi из схемы (9.12) можно найти методом прогонки
Если Поскольку a1 = 0, то по индукции мы получаем, во-первых разрешимость схемы (9.12) в виде (9.15) и во-вторых, справедливость неравенства Учитывая, что zN = 0, получаем соотношение Воспользуемся теперь рекуррентной формулой (9.14) для
Тогда Поскольку
т.к. Переходя к норме, получаем
Дата добавления: 2015-01-18 | Просмотры: 850 | Нарушение авторских прав |
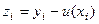
 (9.11)
(9.11) ,
, 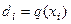 ,
,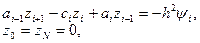 (9.12)
(9.12)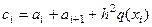 .
.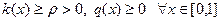
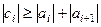 (9.13)
(9.13)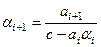 ,
, 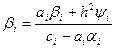 ,
, 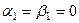 ,
, 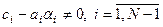 (9.14)
(9.14)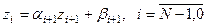 (9.15)
(9.15)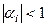 , то
, то 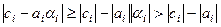 . И тогда из (9.13) и (9.14) следует
. И тогда из (9.13) и (9.14) следует 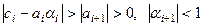 .
.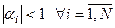 . Следовательно, из (9.15) можно вывести неравенство
. Следовательно, из (9.15) можно вывести неравенство 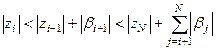 .
. .
.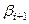 , умножив ее на положительную величину
, умножив ее на положительную величину  :
: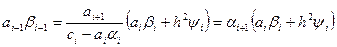
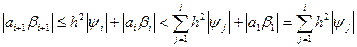 , т.к.
, т.к. 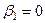
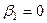 .
.
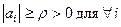 , то
, то 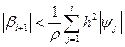 . Т.о. для погрешности в узлах сетки zi можно записать неравенство
. Т.о. для погрешности в узлах сетки zi можно записать неравенство , для
, для 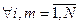 ,
,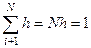 .
. , т.е. разностная схема (9.7) для краевой задачи (9.3)-(9.4) при условиях на коэффициенты (9.10) имеет второй порядок сходимости.
, т.е. разностная схема (9.7) для краевой задачи (9.3)-(9.4) при условиях на коэффициенты (9.10) имеет второй порядок сходимости.