|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
П. 1.2. Интерполяционная формула Лагранжа
Прочитайте:
- Антигенная структура бактерий. Групповые, ввдовые, типовые антигены. Перекрестнореагируюшие антигены. Антигенная формула.
- Групповая зубная формула постоянных и молочных зуов.
- Зубы (строение, сроки прорезывания, формула, кровоснабжение, иннервация). Прикус. Молочные и постоянные зубы.
- Зубы молочные и постоянные, зубная формула, иннервация , кровоснабжение, лимфоотток.
- К/ф «Формула любви»
- Лейкоцитарная формула
- Лейкоциты, их морфофункциональная характеристика, количество, функции, методы подсчета. Лейкоцитарная формула, метод ее определения.
- Международная формула зубов.
- Невменяемость: понятие, критерии. Формула невменяемости. Ограниченная вменяемость.
- Оценка физического и полового развития детей и подростков (морфограмма, половая формула).
|
|
Интерполяционная формула Лагранжа позволяет представить многочлен  в виде линейной комбинации значений функции в виде линейной комбинации значений функции  в узлах интерполирования в узлах интерполирования
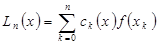 (1.4) (1.4)
Найдем явное выражение для коэффициентов 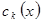 . Из условий интерполирования (1.3) получаем . Из условий интерполирования (1.3) получаем
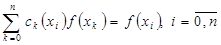
Эти соотношения будут выполнены, если на функции 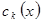 наложить условие наложить условие
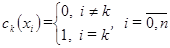
Они означают, что каждая из функций 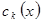 , , 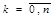
Имеет не менее 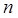 нулей на нулей на  . Поскольку . Поскольку  многочлен степени многочлен степени 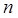 , коэффициенты , коэффициенты 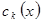 естественно искать также в виде многочлена степени естественно искать также в виде многочлена степени 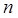 , а именно в виде , а именно в виде
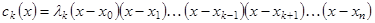
Из условия 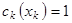 находим находим
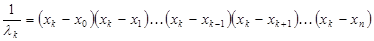
Таким образом, коэффициенты 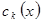 интерполяционного многочлена (1.4) находятся по формулам интерполяционного многочлена (1.4) находятся по формулам
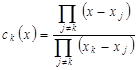 (1.5) (1.5)
Часто коэффициенты 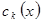 записываются в другом виде. Введем многочлен записываются в другом виде. Введем многочлен  степени степени  : :
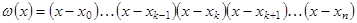 (1.6) (1.6)
и вычислим его производные в точке 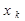 : :
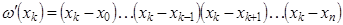 (1.7) (1.7)
Тогда получим, что
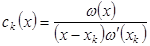 (1.8) (1.8)
Итак, интерполяционный многочлен Лагранжа имеет вид
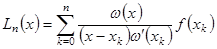 (1.9) (1.9)
или, более подробно,
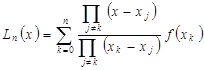 (1.10) (1.10)
Дата добавления: 2015-01-18 | Просмотры: 637 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|
