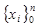|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
П. 1.1. Определение интерполяционного многочленаПусть на отрезке
значения которого в заданных точках Для любой непрерывной функции
Определитель этой системы (определитель Вандермонда) отличен от нуля, если среди точек
Отсюда следует, что такой многочлен существует и он единственен. Определение 1.1 Многочлен
называется интерполяционным многочленом для функции Решение системы (1.2) можно записать различным образом. Наиболее употребительна запись интерполяционного многочлена в форме Лагранжа и в форме Ньютона. Дата добавления: 2015-01-18 | Просмотры: 637 | Нарушение авторских прав |
 заданы точки
заданы точки  (будем называть их узлами интерполирования), в которых известны значения функции
(будем называть их узлами интерполирования), в которых известны значения функции  . Задача интерполирования алгебраическими многочленами состоит в том, чтобы построить многочлен степени
. Задача интерполирования алгебраическими многочленами состоит в том, чтобы построить многочлен степени 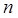
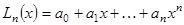 , (1.1)
, (1.1)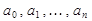 получаем систему линейных уравнений
получаем систему линейных уравнений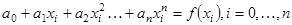 (1.2)
(1.2)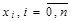 нет совпадающих:
нет совпадающих: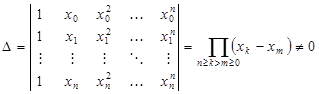
 , удовлетворяющий условию
, удовлетворяющий условию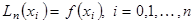 (1.3)
(1.3)