 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Интегрирование случайных процессов по мартингалам, имеющим ограниченную вариацию7.1. Пусть Теорема 29. Пусть Доказательство. Утверждение а) теоремы очевидно. Установим б). Надо показать, что при По теореме Лебега о можарируемой сходимости, имеем, в силу свойств условного математического ожидания, P - п. н.
Доказательство закончено. 7.3. Приведем ряд утверждений вытекающих из теоремы29. Теорема 30 (Кэмбелл). Пусть Доказательство. Нам надо установить равенство
Заметим, что Пример. Пусть
Возьмём математическое ожидание относительно левой и правой частей (6), учитывая (5), имеем Задача. Пусть
Дата добавления: 2015-01-18 | Просмотры: 799 | Нарушение авторских прав |
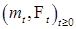 - мартингал, имеющий интегрируемую вариацию. Пусть
- мартингал, имеющий интегрируемую вариацию. Пусть  - ограниченный предсказуемый случайный процесс. Тогда определен P - п. н. интеграл Римана - Стилтьеса от предсказуемой функции h по мартингалу m:
- ограниченный предсказуемый случайный процесс. Тогда определен P - п. н. интеграл Римана - Стилтьеса от предсказуемой функции h по мартингалу m:  , где
, где 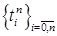 - разбиение отрезка
- разбиение отрезка  , такое, что
, такое, что 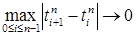 при
при 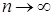 . Из этого построения следует, что
. Из этого построения следует, что  - измерим.
- измерим. . Тогда определён интеграла Римана - Стилтьеса
. Тогда определён интеграла Римана - Стилтьеса  , являющийся: а) при каждом t
, являющийся: а) при каждом t  - измеримой случайной величиной; б) мартингалом относительно потока
- измеримой случайной величиной; б) мартингалом относительно потока  и меры Р.
и меры Р.
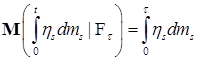 P - п. н. Очевидно, что это равенство эквивалентно следующему
P - п. н. Очевидно, что это равенство эквивалентно следующему  . Действительно, пусть
. Действительно, пусть  .
.
 Последнее равенство следует из того факта, что P - п. н.
Последнее равенство следует из того факта, что P - п. н.  .
.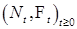 - считывающий процесс, а
- считывающий процесс, а  его компенсатор относительно меры Р. Пусть
его компенсатор относительно меры Р. Пусть  .
. (5)
(5) - мартингал, имеющий интегрируемую вариацию, поэтому (5) следует из теоремы 29.
- мартингал, имеющий интегрируемую вариацию, поэтому (5) следует из теоремы 29.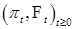 пуассоновский процесс с интенсивностью
пуассоновский процесс с интенсивностью 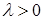 . Найдём его характеристическую функцию. Заметим, сначала, что
. Найдём его характеристическую функцию. Заметим, сначала, что  - мартингал относительно меры P. К функции
- мартингал относительно меры P. К функции 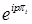 применим формулу Ито (4), имеем
применим формулу Ито (4), имеем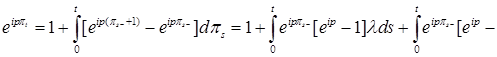
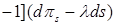 (6)
(6) . Заметим теперь, что
. Заметим теперь, что  . В силу теоремы Фубини имеем:
. В силу теоремы Фубини имеем:  . Отсюда следует, что
. Отсюда следует, что  .
. ,
,  - интенсивность
- интенсивность  -измеримая. Такой точечный процесс называется процессом Кокса. Докажите, что
-измеримая. Такой точечный процесс называется процессом Кокса. Докажите, что 
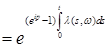 P – п. н. для
P – п. н. для 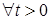 .
.