Свойства компенсаторов точечных процессов. Случайная замена времени
8.1. Теорема 31. Справедливы утверждения.
1) Компенсатор 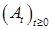 точечного процесса точечного процесса 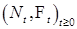 допускает единственное разложение допускает единственное разложение 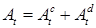 , где , где 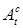 - непрерывная составляющая, - непрерывная составляющая,  - разрывная составляющая. - разрывная составляющая.
2) 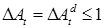 Р - п. н. Р - п. н.
3)  P – п. н. для любого t. P – п. н. для любого t.
Доказательство. 1) Первое утверждение теоремы следует из теоремы 24.
2) Так как  , то , то  . Заметим, что . Заметим, что  - измерим, поэтому - измерим, поэтому  . Так как . Так как  , то , то  Р - п. н. Р - п. н.
3) Сначала заметим, что Р – п. н.
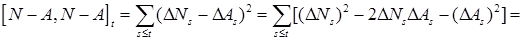
  . .
Так как  является мартингалом, a является мартингалом, a 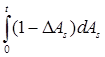 - предсказуемый возрастающий процесс. Поэтому из теоремы Дуба - Мейера следует третье утверждение. Теорема доказана. - предсказуемый возрастающий процесс. Поэтому из теоремы Дуба - Мейера следует третье утверждение. Теорема доказана.
8.2. Пусть 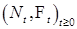 - точечный процесс, а - точечный процесс, а  - его компенсатор, где - его компенсатор, где  - измеримая функция. - измеримая функция.
Теорема 32. Пусть Р - п. н.  . Пусть существует функция . Пусть существует функция
 , обозначаемая через , обозначаемая через  , такая, что , такая, что 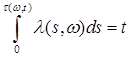 . Тогда . Тогда 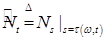 - стандартный пуассоновский процесс (т. е. интенсивность его равна единице). - стандартный пуассоновский процесс (т. е. интенсивность его равна единице).
Доказательство. Сначала покажем, что процесс  имеет компенсатор t, т. е. имеет компенсатор t, т. е.  - мартингал относительно потока - мартингал относительно потока  и меры Р. Пусть и меры Р. Пусть  - ограниченный предсказуемый процесс, тогда имеем, в силу теоремы 30, - ограниченный предсказуемый процесс, тогда имеем, в силу теоремы 30,  . .
Покажем теперь, что  . Очевидно, что . Очевидно, что  - точечный процесс, поэтому - точечный процесс, поэтому  . Отсюда следует, что . Отсюда следует, что  . Значит . Значит 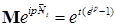 . Доказательство закончено. . Доказательство закончено.
§9 Мультивариантные точечные процессы.
9.1. Определение. Мультивариантным точечным процессом на  называется последовательность называется последовательность 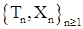 , где , где 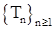 - марковские моменты такие, что: а) - марковские моменты такие, что: а) 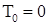 ; б) ; б)  на множестве на множестве  ; в) ; в) 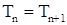 на множестве на множестве  ; а ; а  на множестве на множестве  и и  на множестве на множестве  где где  - некоторая "фиктивная" точка, причём - некоторая "фиктивная" точка, причём  для для  . .
По мультивариантному точечному процессу  легко построить опциональный случайный процесс легко построить опциональный случайный процесс  с кусочно-постоянными траекториями. Действительно, для любого n положим с кусочно-постоянными траекториями. Действительно, для любого n положим
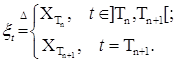
Очевидно, что таким образом построенный случайный процесс  является согласованным и его траектории непрерывны справа и имеют конечный левый предел, т. е. принадлежат пространству Скорохода. является согласованным и его траектории непрерывны справа и имеют конечный левый предел, т. е. принадлежат пространству Скорохода.
Обозначим  - число попаданий мультивариантного точечного процесса в множество - число попаданий мультивариантного точечного процесса в множество  за время t. Очевидно, что за время t. Очевидно, что  считающий процесс, поэтому считающий процесс, поэтому  - субмартингал (относительно меры Р). Стало быть, по теореме Дуба-Мейера существует единственный предсказуемый возрастающий процесс - субмартингал (относительно меры Р). Стало быть, по теореме Дуба-Мейера существует единственный предсказуемый возрастающий процесс  такой, что такой, что  мартингал, т. е. - компенсатор. мартингал, т. е. - компенсатор.
Определение. Пусть Е - конечное или счётное множество, причем 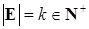 , в этом случае мультивариантный точечный процесс будем называть k-вариантным. , в этом случае мультивариантный точечный процесс будем называть k-вариантным.
9.3. Пусть  , где , где  опциональный процесс построенный по мультивариантному точечному процессу с кусочно-постоянными со значениями в Е, где Е - конечное или счетное множество. Через опциональный процесс построенный по мультивариантному точечному процессу с кусочно-постоянными со значениями в Е, где Е - конечное или счетное множество. Через  обозначим элементы множества Е и назовем их состояниями. Пусть обозначим элементы множества Е и назовем их состояниями. Пусть  - одноточечное множество, т.е. - одноточечное множество, т.е.  . Через . Через  обозначим число попаданий процесса обозначим число попаданий процесса  за время t в состояние i. Очевидно, что: 1) за время t в состояние i. Очевидно, что: 1)  , 2) , 2)  , где , где 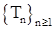 марковские моменты такие, что марковские моменты такие, что 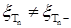 . Справедливо утверждение. . Справедливо утверждение.
Предложение 33. Пусть 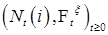 - считающий процесс. Тогда для любых - считающий процесс. Тогда для любых  и и 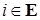 Р - п. н. справедливы представления: Р - п. н. справедливы представления:
1)если  , то , то
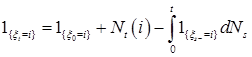 , ,
где  , ,
2) 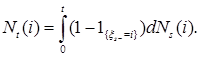
Доказательство. 1) Так как 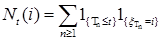 , то, очевидно, что P – п. н. для любых , то, очевидно, что P – п. н. для любых  , , 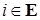
 . .
Получившееся равенство перепишем в виде интеграла Римана-Стилтьеса, имеем P – п. н.  . .
Отсюда следует первое утверждение предложения.
2) Так как марковские моменты  нагружают процесс нагружают процесс  , то , то 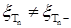 P – п. н. для любого P – п. н. для любого  . Поэтому . Поэтому  P – п. н. для любого P – п. н. для любого  . Следовательно, P – п. н. для любых . Следовательно, P – п. н. для любых  , , 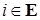 , имеем , имеем
 Последнее равенство перепишем в виде интеграла Римана – Стилтьеса, имеем P – п. н. Последнее равенство перепишем в виде интеграла Римана – Стилтьеса, имеем P – п. н.  . Доказательство закончено. . Доказательство закончено.
Дата добавления: 2015-01-18 | Просмотры: 971 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

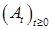 точечного процесса
точечного процесса 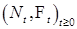 допускает единственное разложение
допускает единственное разложение 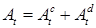 , где
, где 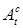 - непрерывная составляющая,
- непрерывная составляющая,  - разрывная составляющая.
- разрывная составляющая.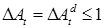 Р - п. н.
Р - п. н. P – п. н. для любого t.
P – п. н. для любого t. , то
, то  . Заметим, что
. Заметим, что  - измерим, поэтому
- измерим, поэтому  . Так как
. Так как  , то
, то  Р - п. н.
Р - п. н.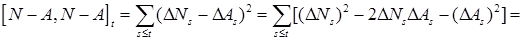

 .
. является мартингалом, a
является мартингалом, a 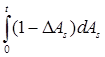 - предсказуемый возрастающий процесс. Поэтому из теоремы Дуба - Мейера следует третье утверждение. Теорема доказана.
- предсказуемый возрастающий процесс. Поэтому из теоремы Дуба - Мейера следует третье утверждение. Теорема доказана. - его компенсатор, где
- его компенсатор, где  - измеримая функция.
- измеримая функция. . Пусть существует функция
. Пусть существует функция , обозначаемая через
, обозначаемая через  , такая, что
, такая, что 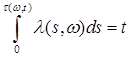 . Тогда
. Тогда 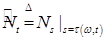 - стандартный пуассоновский процесс (т. е. интенсивность его равна единице).
- стандартный пуассоновский процесс (т. е. интенсивность его равна единице). имеет компенсатор t, т. е.
имеет компенсатор t, т. е.  - мартингал относительно потока
- мартингал относительно потока  и меры Р. Пусть
и меры Р. Пусть  - ограниченный предсказуемый процесс, тогда имеем, в силу теоремы 30,
- ограниченный предсказуемый процесс, тогда имеем, в силу теоремы 30,  .
. . Очевидно, что
. Очевидно, что  - точечный процесс, поэтому
- точечный процесс, поэтому  . Отсюда следует, что
. Отсюда следует, что  . Значит
. Значит 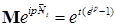 . Доказательство закончено.
. Доказательство закончено. называется последовательность
называется последовательность 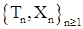 , где
, где 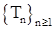 - марковские моменты такие, что: а)
- марковские моменты такие, что: а) 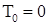 ; б)
; б)  на множестве
на множестве  ; в)
; в) 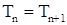 на множестве
на множестве  ; а
; а  на множестве
на множестве  на множестве
на множестве  - некоторая "фиктивная" точка, причём
- некоторая "фиктивная" точка, причём  для
для  .
. легко построить опциональный случайный процесс
легко построить опциональный случайный процесс  с кусочно-постоянными траекториями. Действительно, для любого n положим
с кусочно-постоянными траекториями. Действительно, для любого n положим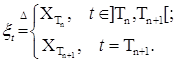
 - число попаданий мультивариантного точечного процесса в множество
- число попаданий мультивариантного точечного процесса в множество  за время t. Очевидно, что
за время t. Очевидно, что  считающий процесс, поэтому
считающий процесс, поэтому  - субмартингал (относительно меры Р). Стало быть, по теореме Дуба-Мейера существует единственный предсказуемый возрастающий процесс
- субмартингал (относительно меры Р). Стало быть, по теореме Дуба-Мейера существует единственный предсказуемый возрастающий процесс  такой, что
такой, что  мартингал, т. е. - компенсатор.
мартингал, т. е. - компенсатор.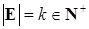 , в этом случае мультивариантный точечный процесс будем называть k-вариантным.
, в этом случае мультивариантный точечный процесс будем называть k-вариантным. , где
, где  опциональный процесс построенный по мультивариантному точечному процессу с кусочно-постоянными со значениями в Е, где Е - конечное или счетное множество. Через
опциональный процесс построенный по мультивариантному точечному процессу с кусочно-постоянными со значениями в Е, где Е - конечное или счетное множество. Через  обозначим элементы множества Е и назовем их состояниями. Пусть
обозначим элементы множества Е и назовем их состояниями. Пусть  - одноточечное множество, т.е.
- одноточечное множество, т.е.  . Через
. Через  обозначим число попаданий процесса
обозначим число попаданий процесса  , 2)
, 2)  , где
, где 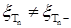 . Справедливо утверждение.
. Справедливо утверждение.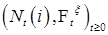 - считающий процесс. Тогда для любых
- считающий процесс. Тогда для любых  и
и 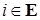 Р - п. н. справедливы представления:
Р - п. н. справедливы представления: , то
, то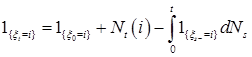 ,
, ,
,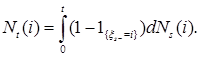
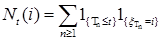 , то, очевидно, что P – п. н. для любых
, то, очевидно, что P – п. н. для любых  ,
,  .
. .
. нагружают процесс
нагружают процесс  . Поэтому
. Поэтому  P – п. н. для любого
P – п. н. для любого  Последнее равенство перепишем в виде интеграла Римана – Стилтьеса, имеем P – п. н.
Последнее равенство перепишем в виде интеграла Римана – Стилтьеса, имеем P – п. н.  . Доказательство закончено.
. Доказательство закончено.