Основные определения. Описание процессов с непрерывным временем
Глава 3. Элементы общей теории случайных процессов. Точечные случайные процессы.
Основные определения. Описание процессов с непрерывным временем.
1.1. Пусть 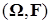 - измеримое пространство. - измеримое пространство.
Определение. Пусть  , а , а  - семейство на - семейство на  -алгебре на -алгебре на 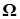 . Семейства . Семейства  назовем потоком назовем потоком  -алгебр или фильтрацией, если для -алгебр или фильтрацией, если для 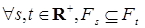 при при 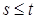 и и 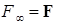 . .
Замечание. Фильтрация  описывает историю некоторого явления, и описывает историю некоторого явления, и 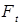 называют называют  -алгебройсобытий предшествующих моменту времени t. -алгебройсобытий предшествующих моменту времени t.
Определение. Будем говорить, что поток  -алгебр -алгебр 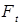 непрерывен справа, если непрерывен справа, если  . .
Определение. Пусть имеется два измеримых пространства 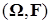 и и  . Случайным процессом с непрерывным временем, определенным на . Случайным процессом с непрерывным временем, определенным на 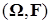 со значениями в со значениями в  называется семейство называется семейство  случайных элементов со значениями в E. Пространство случайных элементов со значениями в E. Пространство 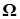 будем называть пространством элементарных исходов, а E - пространством состояний. будем называть пространством элементарных исходов, а E - пространством состояний.
Для 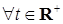 значение значение  называется состоянием случайного процесса в момент времени называется состоянием случайного процесса в момент времени  . Для фиксированного . Для фиксированного  множество множество 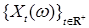 называется траекторией или реализацией случайного процесса. называется траекторией или реализацией случайного процесса.
Определение. Случайный процесс  называется согласованным с фильтрацией называется согласованным с фильтрацией  , если при каждом , если при каждом  он он 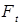 -измерим, для него будем использовать обозначение -измерим, для него будем использовать обозначение  . .
Определение.  - вероятностное пространство с фильтрацией - вероятностное пространство с фильтрацией  называется стохастическим базисом, если называется стохастическим базисом, если 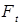 - непрерывно справа и для него будем использовать обозначение - непрерывно справа и для него будем использовать обозначение 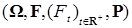 . .
Соглашение: будем полагать везде ниже, что стохастический базис полный, т.е.  -алгебра F и фильтрация -алгебра F и фильтрация 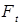 (для (для 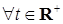 ) пополнены множествами нулевой меры P. ) пополнены множествами нулевой меры P.
1.2. Определение. Случайный процесс  называется измеримым, если отображение называется измеримым, если отображение  измеримо относительно измеримо относительно  -алгебры -алгебры  . .
Определение. Случайный процесс  называется прогрессивно измеримым, если отображение называется прогрессивно измеримым, если отображение  измеримо относительно измеримо относительно  . .
Замечание. Отметим, что всякий прогрессивно измеримый процесс является согласованным. Обратное утверждение неверно. Однако верно следующее утверждение.
Теорема 1. Пусть  - согласованный процесс и Е - польское пространство. Тогда - согласованный процесс и Е - польское пространство. Тогда  - прогрессивно измерим. - прогрессивно измерим.
Доказательство. Для 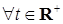 рассмотрим диадическое разбиение отрезка рассмотрим диадическое разбиение отрезка  , т. е. разбиение , т. е. разбиение  на на  равных интервала, где равных интервала, где  . Для . Для  , положим , положим  . Очевидно, что . Очевидно, что 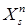 - измеримое отображение из - измеримое отображение из  относительно относительно  -алгебры -алгебры  . Устремляя . Устремляя 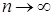 получаем, что отображение получаем, что отображение  является измеримым относительно является измеримым относительно  -алгебры -алгебры  при каждом при каждом  .. ..
1.3. Определение. Пусть  и и  - два случайных процесса, определенных на - два случайных процесса, определенных на  . Процесс . Процесс  называется модификацией процесса называется модификацией процесса  , если для каждого , если для каждого 
Р - п. н.
Определение. Два случайных процесса, определенные на  , называются неотличимыми, если Р - п. н. для всех , называются неотличимыми, если Р - п. н. для всех  . .
Замечание. В определении модификации множество нулевой меры Р, на котором отличаются  и и  может зависеть от может зависеть от  , в то время как в определении неотличимых процессов существует только одно множество меры нуль, вне которого , в то время как в определении неотличимых процессов существует только одно множество меры нуль, вне которого  для всех для всех  . Поясним это на примере. Пусть . Поясним это на примере. Пусть  - мера Лебега на - мера Лебега на  , а , а 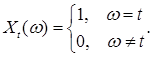 Тогда ясно, что Тогда ясно, что 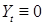 - модификация - модификация  , хотя неотличимости нет, так как , хотя неотличимости нет, так как  . .
1.4. Теперь приведем без доказательства достаточные условия существования у процесса  модификаций принадлежащих пространствам модификаций принадлежащих пространствам  и и  , соответственно. , соответственно.
Теорема 2. Пусть  случайный процесс со значениями в случайный процесс со значениями в 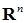 . Если при всех . Если при всех  существуют константы существуют константы  такие, что такие, что
 (1) (1)
то процесс  имеет непрерывную модификацию. имеет непрерывную модификацию.
Теорема 3. Пусть  случайный процесс со значениями в случайный процесс со значениями в 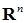 . Если для любого . Если для любого  существуют константы существуют константы  такие, что такие, что  где где  , то у процесса , то у процесса  существует модификация из существует модификация из  . .
1.5. Определение. Случайный процесс  называется стохастически непрерывным справа (слева) в точке называется стохастически непрерывным справа (слева) в точке  , если для любого , если для любого 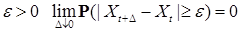 ( ( ). ).
Случайный процесс  называется стохастически непрерывным справа (слева), если он стохастически непрерывен справа (слева) в любой точке называется стохастически непрерывным справа (слева), если он стохастически непрерывен справа (слева) в любой точке  . .
Определение. Если  , то будем говорить, что процесс принадлежит классу , то будем говорить, что процесс принадлежит классу  . .
Определение. Процесс  непрерывен справа (слева) в среднем порядка непрерывен справа (слева) в среднем порядка 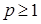 в точке t, если в точке t, если  . Процесс . Процесс  непрерывен справа (слева) в среднем порядка p, если он непрерывен справа (слева) в среднем порядка p, в каждой точке непрерывен справа (слева) в среднем порядка p, если он непрерывен справа (слева) в среднем порядка p, в каждой точке  . .
Теорема 4. Если процесс  - непрерывен справа (слева) в точке t в среднем порядка p, то он стохастически непрерывен справа (слева) в точке t. - непрерывен справа (слева) в точке t в среднем порядка p, то он стохастически непрерывен справа (слева) в точке t.
Доказательство следует из неравенства Чебышева. Действительно пусть любое  , имеем , имеем  . Переходя к пределу при . Переходя к пределу при  получаем утверждение теоремы. получаем утверждение теоремы.
1.6. Пример (пуассоновский процесс). Пусть имеется  последовательность независимых в совокупности, одинаково распределенных случайных величин, имеющих экспоненциальное распределение с параметром последовательность независимых в совокупности, одинаково распределенных случайных величин, имеющих экспоненциальное распределение с параметром 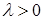 . Пусть . Пусть  . Положим . Положим  . Очевидно, что . Очевидно, что  Р - п. н. для Р - п. н. для  . Пусть . Пусть  . Очевидно, что . Очевидно, что 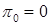 . Таким образом определенный процесс . Таким образом определенный процесс  называется пуассоновским. Из приведенных выше построений следует, что называется пуассоновским. Из приведенных выше построений следует, что  непрерывен справа. непрерывен справа.
Найдем распределение вероятностей  . Ясно, что . Ясно, что  , где , где

Очевидно

Поэтому 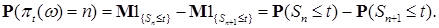 (2) (2)
Обозначим через  - экспоненциальное распределение с параметром - экспоненциальное распределение с параметром  , а через , а через  - n-кратную свертку этих распределений. Очевидно, что - n-кратную свертку этих распределений. Очевидно, что  , а , а  Поэтому из (2) имеем: Поэтому из (2) имеем:  . .
Вычислим  , имеем , имеем
 . .
Теперь вычислим 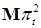 , имеем , имеем
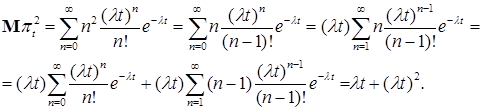
Отсюда следует, что дисперсия пуассоновского процесса в момент времени  равна равна  . Отметим, что величина . Отметим, что величина 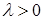 - называется интенсивностью пуассоновского процесса. - называется интенсивностью пуассоновского процесса.
Вопрос: Является ли пуассоновский процесс непрерывным в среднем порядка 1? Ответ положительный.
Действительно, так как  - неубывающий процесс, т.е. - неубывающий процесс, т.е.  Р - п. н. Поэтому Р - п. н. Поэтому  Следовательно, процесс Следовательно, процесс  непрерывен в среднем порядка 1 для непрерывен в среднем порядка 1 для 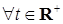 , а в силу теоремы 4 пуассоновский процесс стохастически непрерывен. , а в силу теоремы 4 пуассоновский процесс стохастически непрерывен.
Дата добавления: 2015-01-18 | Просмотры: 1190 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|

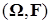 - измеримое пространство.
- измеримое пространство. , а
, а  - семейство на
- семейство на  -алгебре на
-алгебре на 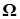 . Семейства
. Семейства  назовем потоком
назовем потоком 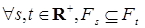 при
при 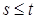 и
и 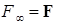 .
.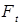 называют
называют  .
. . Случайным процессом с непрерывным временем, определенным на
. Случайным процессом с непрерывным временем, определенным на  случайных элементов со значениями в E. Пространство
случайных элементов со значениями в E. Пространство 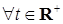 значение
значение  называется состоянием случайного процесса в момент времени
называется состоянием случайного процесса в момент времени  . Для фиксированного
. Для фиксированного  множество
множество 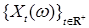 называется траекторией или реализацией случайного процесса.
называется траекторией или реализацией случайного процесса. .
. - вероятностное пространство с фильтрацией
- вероятностное пространство с фильтрацией 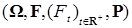 .
. называется измеримым, если отображение
называется измеримым, если отображение  измеримо относительно
измеримо относительно  .
. измеримо относительно
измеримо относительно  .
. , т. е. разбиение
, т. е. разбиение  равных интервала, где
равных интервала, где  . Для
. Для  , положим
, положим  . Очевидно, что
. Очевидно, что 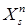 - измеримое отображение из
- измеримое отображение из  относительно
относительно 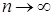 получаем, что отображение
получаем, что отображение  является измеримым относительно
является измеримым относительно  - два случайных процесса, определенных на
- два случайных процесса, определенных на 
 .
. для всех
для всех  - мера Лебега на
- мера Лебега на  , а
, а 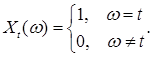 Тогда ясно, что
Тогда ясно, что 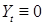 - модификация
- модификация  , хотя неотличимости нет, так как
, хотя неотличимости нет, так как  .
. модификаций принадлежащих пространствам
модификаций принадлежащих пространствам  и
и  , соответственно.
, соответственно.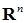 . Если при всех
. Если при всех  существуют константы
существуют константы  такие, что
такие, что (1)
(1) существуют константы
существуют константы  такие, что
такие, что  где
где  , то у процесса
, то у процесса 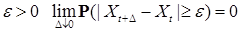 (
( ).
). , то будем говорить, что процесс принадлежит классу
, то будем говорить, что процесс принадлежит классу  .
.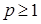 в точке t, если
в точке t, если  . Процесс
. Процесс  , имеем
, имеем  . Переходя к пределу при
. Переходя к пределу при  получаем утверждение теоремы.
получаем утверждение теоремы. последовательность независимых в совокупности, одинаково распределенных случайных величин, имеющих экспоненциальное распределение с параметром
последовательность независимых в совокупности, одинаково распределенных случайных величин, имеющих экспоненциальное распределение с параметром 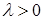 . Пусть
. Пусть  . Положим
. Положим  . Очевидно, что
. Очевидно, что  Р - п. н. для
Р - п. н. для  . Пусть
. Пусть  . Очевидно, что
. Очевидно, что 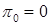 . Таким образом определенный процесс
. Таким образом определенный процесс  называется пуассоновским. Из приведенных выше построений следует, что
называется пуассоновским. Из приведенных выше построений следует, что  . Ясно, что
. Ясно, что  , где
, где 

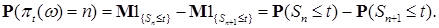 (2)
(2) - экспоненциальное распределение с параметром
- экспоненциальное распределение с параметром  , а через
, а через  - n-кратную свертку этих распределений. Очевидно, что
- n-кратную свертку этих распределений. Очевидно, что  , а
, а  Поэтому из (2) имеем:
Поэтому из (2) имеем:  .
. , имеем
, имеем .
.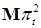 , имеем
, имеем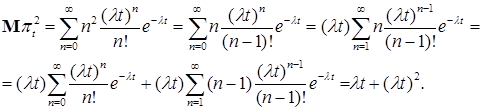
 . Отметим, что величина
. Отметим, что величина  - неубывающий процесс, т.е.
- неубывающий процесс, т.е.  Р - п. н. Поэтому
Р - п. н. Поэтому  Следовательно, процесс
Следовательно, процесс