 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Разрешимость системы уравнений Колмогорова для процессов с конечным или счетным числом состояний11.1. Теорема 37. Пусть 2) Доказательство теоремы 37 опирается на лемму. Лемма 38 (Гронуолла - Беллмана). Пусть Доказательство. Очевидно неравенство для Последнее можно переписать в виде Доказательство теоремы 37. Сначала заметим, что (10) можно переписать в виде
Отсюда, в силу формулы Коши (для обыкновенного линейного неоднородного уравнения первого порядка), имеем
Заметим, что
Отсюда в силу теоремы Фубини следует, что
(Здесь мы учли, что Таким образом, мы пришли к неравенству
В силу леммы Гронуолла - Беллмана, имеем Отсюда следует существование решения системы уравнений (10). Установим теперь единственность решения системы (10). Пусть
Обозначим
Отсюда, в силу теоремы Фубини, имеем для любого t
Поэтому, в силу леммы Гронуолла - Беллмана, имеем 11.2. Приведем теперь условия, при выполнении которых решение системы (10) имеет вероятностный смысл. Теорема 39. Пусть выполняются условия: а) для и б) Тогда для 1) для любых 2) если Доказательство. 1) Из доказательства теоремы 37 следует, что
Тогда из (11) имеем Итерируя это равенство, имеем
Отсюда следует, что Покажем теперь, что для
Поэтому, в силу того что Замечание. Процесс 11.3. Докажем теперь утверждение обратное к теореме 35. Теорема 40. Пусть
где Доказательство. Покажем сначала, что процесс
Так как для любых
Возьмем условное математическое ожидание
В силу условий теоремы
Отсюда следует утверждение теоремы. Доказательство закончено.
Дата добавления: 2015-01-18 | Просмотры: 902 | Нарушение авторских прав |
 - размера
- размера  матрица интенсивности перехода такая, что: 1)
матрица интенсивности перехода такая, что: 1)  для
для  и
и  ,
,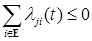 для
для  , 3)
, 3)  . Тогда в классе
. Тогда в классе  решение уравнения (10) существует и единственно.
решение уравнения (10) существует и единственно. ,
,  - измеримая функция, обозначаемые через u (t) и c (s), соответственно, такие, что: а)
- измеримая функция, обозначаемые через u (t) и c (s), соответственно, такие, что: а)  ; б)
; б) 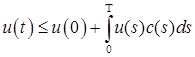 . Тогда для
. Тогда для  справедливо неравенство
справедливо неравенство  .
. .
. . Отсюда следует, что
. Отсюда следует, что 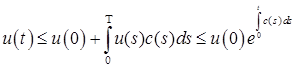 . Доказательство закончено.
. Доказательство закончено. .
.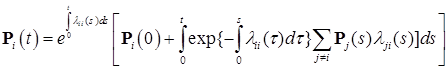 . (11)
. (11) , поэтому имеем неравенства:
, поэтому имеем неравенства: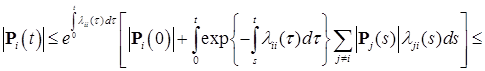
 .
.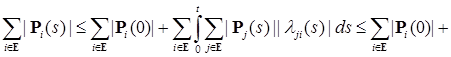
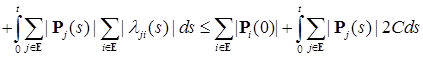 .
. для
для  ).
). .
.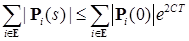 .
. , l = 1,2, - два решения системы (10). Поэтому в силу (11) для
, l = 1,2, - два решения системы (10). Поэтому в силу (11) для  . (12)
. (12) . Из (12) следуют неравенства
. Из (12) следуют неравенства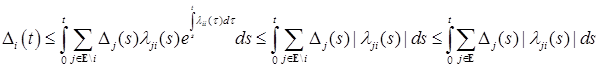 .
. .
. . Отсюда следует утверждение теоремы.
. Отсюда следует утверждение теоремы.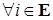
 и
и 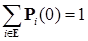 ;
; - матрица интенсивности перехода.
- матрица интенсивности перехода. и
и  ;
; для любых
для любых  и
и  , то
, то  для
для  допускает представление (11). Обозначим
допускает представление (11). Обозначим .
. .
.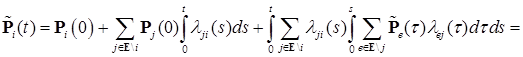
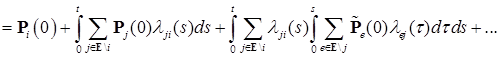 .
. представляет собой ряд, слагаемые которого неотрицательны (в силу условий теоремы). Поэтому для
представляет собой ряд, слагаемые которого неотрицательны (в силу условий теоремы). Поэтому для 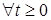
 . Так как
. Так как 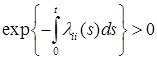 , то и
, то и 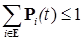 . Из уравнения (10) следует, что, в силу теоремы Фубини,
. Из уравнения (10) следует, что, в силу теоремы Фубини, . (13)
. (13) , получаем
, получаем  для
для  . Доказательство закончено.
. Доказательство закончено. , матрица интенсивности которого удовлетворяет условию
, матрица интенсивности которого удовлетворяет условию 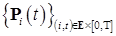 удовлетворяет системе уравнений (10). Пусть выполнены условия теоремы 37. Тогда для
удовлетворяет системе уравнений (10). Пусть выполнены условия теоремы 37. Тогда для  P - п. н. справедливо представление
P - п. н. справедливо представление , (9')
, (9') - ограниченный мартингал.
- ограниченный мартингал. - ограничен. Действительно,
- ограничен. Действительно, .
. и
и  , то
, то  . Докажем теперь, что
. Докажем теперь, что  является мартингалом, т. е.
является мартингалом, т. е. . Из (9') следует, что P – п. н.
. Из (9') следует, что P – п. н.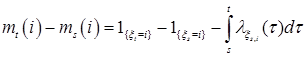 . (9а)
. (9а) относительно левой и правой частей (9а), имеем в силу теоремы Фубини:
относительно левой и правой частей (9а), имеем в силу теоремы Фубини: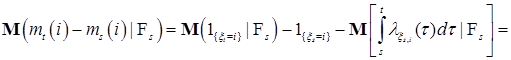
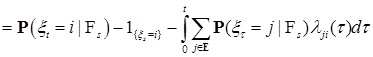 .
. допускает представление
допускает представление .
.